Understanding The 30 60 90 Triangle: Sides, Ratios, And Solutions

Lew Rohan DDS 25 Aug 2025

Have you ever felt like geometry problems take ages to solve, or that you are always getting tangled up in decimal answers when you really want something precise? Well, for many, there is a special kind of triangle that can actually make things much simpler, offering powerful relationships between its angles and sides. This particular shape, known as the 30 60 90 triangle, is a true shortcut for anyone working with right triangles, you know, the ones with a 90-degree angle. It's a bit like having a secret code for certain math challenges, and honestly, it helps quite a bit.

You see, some triangles are just naturally more interesting than others, and this one, with its angles of 30 degrees, 60 degrees, and 90 degrees, really stands out. It’s a special right triangle where the angles measure exactly those amounts, and because of this, its sides always keep a consistent ratio. This consistent ratio is what makes it so useful, allowing you to find missing side lengths without too much fuss, which is pretty cool, if you ask me.

Today, we're going to explore this amazing geometric shape. We'll learn what a 30 60 90 triangle is, how you can easily spot it, and how to use its special side lengths and angles to solve problems. We'll also look at the 30 60 90 theorem formula, and even see some examples so you can truly understand how to use it in your math problems. So, in a way, get ready to make your geometry work a whole lot faster and, honestly, more accurate.

What Exactly is a 30 60 90 Triangle?
The Consistent Magic of the 30 60 90 Triangle Ratio
Why These Triangles Are So Useful
Spotting a 30 60 90 Triangle
The 30 60 90 Triangle Rules and Formula
Solving Problems with Your New Knowledge
Real-World Uses for the 30 60 90 Triangle
Quick Tips and Tools for Success
Frequently Asked Questions About the 30 60 90 Triangle
Final Thoughts on the 30 60 90 Triangle

What Exactly is a 30 60 90 Triangle?

At its core, a 30 60 90 triangle is a special right triangle, which is to say it has one angle that measures exactly 90 degrees. What makes it extra special, though, is that its other two angles are fixed at 30 degrees and 60 degrees. This is pretty straightforward, you know, because the sum of the internal angles of any triangle is always 180 degrees. So, if you have a 90-degree angle and a 30-degree angle, the third angle simply has to be 60 degrees, and that's just how it works.

These triangles are, in some respects, truly special in geometry. They have powerful relationships that unfold when you start studying their angles and sides. This means that if you know just one side length, or perhaps even just a bit about one side, you can figure out all the other parts of the triangle. It's almost like a little puzzle where knowing one piece helps you put everything else together, which is pretty handy.

The Consistent Magic of the 30 60 90 Triangle Ratio

The real secret, the actual magic behind the 30 60 90 triangle, is its consistent side ratio. The sides opposite these specific angles follow a very particular pattern. This pattern remains the same across all triangles of this type, no matter how big or small they are. It’s a bit like a universal rule for these shapes, and it's something you can really count on.

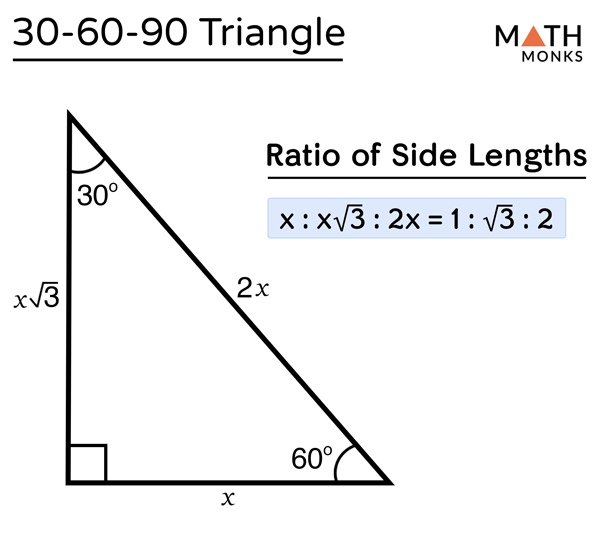
Here’s how the ratio generally works: if the side opposite the 30-degree angle has a length of 'x', then the side opposite the 60-degree angle will be 'x√3', and the side opposite the 90-degree angle (which is the hypotenuse) will be '2x'. This consistent relationship is what we call the 30 60 90 triangle rule, and it's honestly quite fundamental. Knowing this ratio is like having a key to quickly solve many geometry questions, making them faster and more accurate, so it's a very useful thing to remember.

Why These Triangles Are So Useful

You might wonder why we even bother with these "special" triangles. Well, one of the biggest reasons is their ability to yield exact answers. When you're dealing with trigonometric functions or other geometry problems, you often end up with long decimal approximations. However, with a 30 60 90 triangle, you can often get precise, exact answers, which is a big deal for accuracy. This means no rounding errors, just pure mathematical truth, you know, which is pretty satisfying.

Furthermore, this knowledge makes solving geometry questions considerably faster. Instead of using the Pythagorean theorem every single time, which you can use to solve for the remaining side, you can simply apply the ratio. This saves a lot of time and effort, especially in exams or when you have many problems to tackle. It's basically a shortcut that doesn't compromise on correctness, and that's something we all appreciate, right?

Spotting a 30 60 90 Triangle

Identifying a 30 60 90 triangle is usually pretty straightforward. The most obvious way, of course, is if the problem directly tells you the angles are 30°, 60°, and 90°. That's the easiest giveaway, you know, like a big sign pointing it out. However, sometimes you might only be given one angle or perhaps a hint about the side lengths.

If you know it's a right triangle (meaning one angle is 90°) and you're given one of the other angles as either 30° or 60°, then you can automatically figure out the third angle. For instance, if you have a right triangle with a 30° angle, the remaining angle must be 60° (180° - 90° - 30° = 60°). So, that's how you can tell. Similarly, if you see a right triangle with a 60° angle, the third angle will be 30°. It's a simple deduction, and it helps you quickly identify this special type of triangle, which is pretty useful, actually.

The 30 60 90 Triangle Rules and Formula

Now, let's get into the heart of it: the specific rules and the 30 60 90 theorem formula that guide these triangles. Understanding these rules is absolutely key to using this special triangle effectively. The sides of this triangle have specific ratios that remain consistent, as we discussed, and knowing these relationships is what gives you the power to solve problems quickly. So, here's how it all breaks down, in a way.

Since it’s a right triangle, the sides touching the right angle are called the legs of the triangle. It has a long leg and a short leg, and the hypotenuse is the side across from the right angle. These terms are important for remembering the ratio, you know, because they describe where each side sits in relation to the angles.

The Short Leg (Opposite 30°)

This is the smallest side of the triangle. It's always found directly across from the 30-degree angle. We often represent its length with the variable 'x'. This 'x' becomes our base unit for finding the other two sides. If you know this side, you're pretty much set to find everything else. It's the starting point, basically, for all your calculations in this type of triangle.

The Long Leg (Opposite 60°)

The long leg is the side across from the 60-degree angle. Its length is always the short leg's length multiplied by the square root of 3. So, if the short leg is 'x', the long leg is 'x√3'. This relationship is a fundamental part of the 30 60 90 triangle formula. It's a bit more than just 'x', but it's still very predictable, which is nice.

The Hypotenuse (Opposite 90°)

The hypotenuse is the longest side of any right triangle, and in a 30 60 90 triangle, it's always found opposite the 90-degree angle. Its length is simply double the length of the short leg. So, if the short leg is 'x', the hypotenuse is '2x'. This relationship is probably the easiest to remember, and it’s a really quick way to find the longest side if you know the shortest one. It's a very clear connection, honestly.

So, to summarize the 30 60 90 triangle rules, the sides are in the ratio of x : x√3 : 2x, corresponding to the sides opposite the 30°, 60°, and 90° angles, respectively. This foundational rule, with its side ratios and shortcuts, is what you need for working with these triangles. It's a powerful tool, you know, for students and professionals alike.

Solving Problems with Your New Knowledge

Let's put these rules into practice with a few examples. Understanding how to use the 30 60 90 triangle formula with solved examples is the best way to grasp it. It makes it all click, in a way, when you see it in action. So, let's consider some common scenarios.

Example 1: Finding Missing Sides When You Know the Short Leg

Imagine you have a 30 60 90 triangle, and the side opposite the 30° angle (the short leg) measures 5 units. How do you find the other two sides?

Short Leg (opposite 30°): x = 5
Long Leg (opposite 60°): x√3 = 5√3
Hypotenuse (opposite 90°): 2x = 2 * 5 = 10

So, the sides are 5, 5√3, and 10. That's pretty quick, isn't it?

Example 2: Finding Missing Sides When You Know the Hypotenuse

Suppose the hypotenuse of a 30 60 90 triangle is 14 units. What are the lengths of the legs?

Hypotenuse (opposite 90°): 2x = 14
To find 'x', divide the hypotenuse by 2: x = 14 / 2 = 7
Short Leg (opposite 30°): x = 7
Long Leg (opposite 60°): x√3 = 7√3

Here, the sides are 7, 7√3, and 14. You can see how knowing one value helps you get all the other parameters, which is quite handy, honestly.

Example 3: Finding Missing Sides When You Know the Long Leg

What if the side opposite the 60° angle (the long leg) is 9√3 units long?

Long Leg (opposite 60°): x√3 = 9√3
To find 'x', divide by √3: x = 9
Short Leg (opposite 30°): x = 9
Hypotenuse (opposite 90°): 2x = 2 * 9 = 18

The sides here are 9, 9√3, and 18. These examples show how applying the formula and the properties of this special type of right triangle can make solving problems much simpler. It's just a matter of knowing the relationships, you know.

Real-World Uses for the 30 60 90 Triangle

These special triangles aren't just for textbooks; they have practical applications in various fields. For instance, find out how to use it in drafting. Architects and engineers frequently use these ratios when designing structures, creating blueprints, or even just making quick calculations on a job site. It helps them ensure angles and proportions are correct without needing complex trigonometric tables or calculators for every measurement. It's a very practical tool, honestly.

You can also see applications in carpentry, where precise angles are needed for cuts, or in surveying, where distances and heights are determined using triangulation. The ability to compute its mean length or quickly find side lengths, area, and even proof of this triangle using the Pythagorean theorem makes it incredibly versatile. This knowledge is perfect for exam preparation, like for CBSE or JEE exams, and it's also great for quick mobile revision. It’s a foundational piece of geometry, and it crops up in many places, which is pretty interesting, I think.

Quick Tips and Tools for Success

To truly get the hang of the 30 60 90 triangle, here are a few pointers and resources. First off, practice is key. The more you work with these triangles, the more natural the ratios will feel. Try drawing them out, maybe even drag the orange dots on each vertex to reshape a triangle in a figure, and note how the angles remain. This visual practice can really help solidify the concept, you know, for better recall.

Another fantastic tool is a 30 60 90 triangle calculator. Our free 30 60 90 triangle calculator solves for all sides, angles, area, and more. You just enter one known value to get all the other parameters. It’s a safe bet for your geometry problems, providing accurate results for students and professionals alike. This means you can check your work or quickly get answers when you're in a pinch, which is very convenient, actually. Learn more about geometry concepts on our site for additional support, and you can also find more resources on special right triangles there. Having these tools makes learning and applying these rules much simpler, so why not use them?

Frequently Asked Questions About the 30 60 90 Triangle

What is the 30 60 90 triangle rule?

The main rule for a 30 60 90 triangle is about its side lengths, you know, in relation to its angles. The sides opposite the 30°, 60°, and 90° angles follow a consistent ratio of x : x√3 : 2x. This means the shortest side (opposite 30°) is 'x', the medium side (opposite 60°) is 'x' times the square root of 3, and the longest side (the hypotenuse, opposite 90°) is 'x' doubled. It's a pretty straightforward pattern, honestly.

How do you find the sides of a 30 60 90 triangle?

To find the sides of a 30 60 90 triangle, you usually need to know the length of just one side. If you know the short leg (x), you multiply it by √3 to get the long leg, and you multiply it by 2 to get the hypotenuse. If you know the hypotenuse, you divide it by 2 to find the short leg, and then multiply that by √3 for the long leg. And if you know the long leg, you divide it by √3 to find the short leg, and then double that for the hypotenuse. It's all about using that consistent ratio, you know, to work backward or forward.

What is the ratio of a 30 60 90 triangle?

The ratio of a 30 60 90 triangle's sides is x : x√3 : 2x. This ratio describes the relationship between the side opposite the 30-degree angle (x), the side opposite the 60-degree angle (x√3), and the side opposite the 90-degree angle (2x). This specific set of relationships is what makes this triangle so special and, honestly, so powerful for solving geometry problems. It's a very predictable pattern, which is great for calculations.

Final Thoughts on the 30 60 90 Triangle

Learning about the 30 60 90 triangle truly gives you a foundational set of rules and shortcuts for working with these special shapes. This knowledge, honestly, makes solving geometry questions faster and more accurate. By understanding its angles, sides, and area formulas, you gain a significant advantage in many math situations. The special nature of these triangles is their ability to yield exact answers instead of decimal approximations, which is a big plus for precision. So, whether you're a student preparing for exams or a professional needing quick calculations, mastering the 30 60 90 triangle is a very valuable skill to have. It's a simple tool, but it's pretty effective, you know, for making your math life a bit easier.

30-60-90 Triangle - Rules, Formula, Theorem, Sides, Examples

30 60 90 triangle - Cuemath

30-60-90 Triangle – Definition, Formulas, Examples

Celeflash News