How To Find Perimeter: Your Easy Guide To Measuring Shapes Today
Have you ever needed to figure out the distance around something, like a garden you want to fence or a room needing new baseboards? That, you know, is where understanding perimeter comes in very handy. The perimeter of a shape, as my text puts it, is defined as the total length of its boundary. It's essentially the measurement of the outline of any closed shape, which is a rather simple concept once you get the hang of it, you'll find.
For many, the idea of calculating anything in math can seem a bit daunting, yet finding perimeter is actually a very straightforward process. It's not about complex equations or tricky theories; it’s really about simple addition, in a way. Whether you're dealing with a perfectly symmetrical square or a shape with many uneven sides, the core idea remains pretty much the same, which is rather comforting.
This guide will show you how to work out perimeter, including what the perimeter of a shape is and how to calculate it for different shapes, as my text explains. We'll also look at perimeter word problems, which are, you know, just real-life scenarios put into numbers. By the end, you'll have a solid grasp on this concept, and it's almost a certainty that you won't need to worry about perimeter calculations anymore, which is good news.
- La Casa De Los Famosos Vota
- In The Clurb We All Fam
- Kendrick Lamar Mustard Song
- How To Get Rid Of Gnats
- Help I Accidentally Summoned Mahoraga
Table of Contents
- What Exactly is Perimeter?
- The Basic Idea: Adding Up Sides
- Finding Perimeter for Common Shapes
- Tackling Perimeter Word Problems
- Why Does Knowing Perimeter Matter?
- Common Questions About Perimeter
What Exactly is Perimeter?
The perimeter is the total length or distance around a two-dimensional shape, that is, what my text tells us. Imagine walking along the edge of a park; the total distance you walk would be the perimeter of that park. It’s the outline, the boundary, the outside edge of any closed figure, you know. This simple definition is actually the key to understanding all perimeter calculations, which is pretty cool.
My text makes it clear: "Perimeter is the total length of the boundary of any closed shape." So, if you have a drawing of a house, the perimeter would be the length of all its outside walls combined, in a way. It's a fundamental concept in geometry, and it's rather useful for many practical things, as you'll see.
The Basic Idea: Adding Up Sides
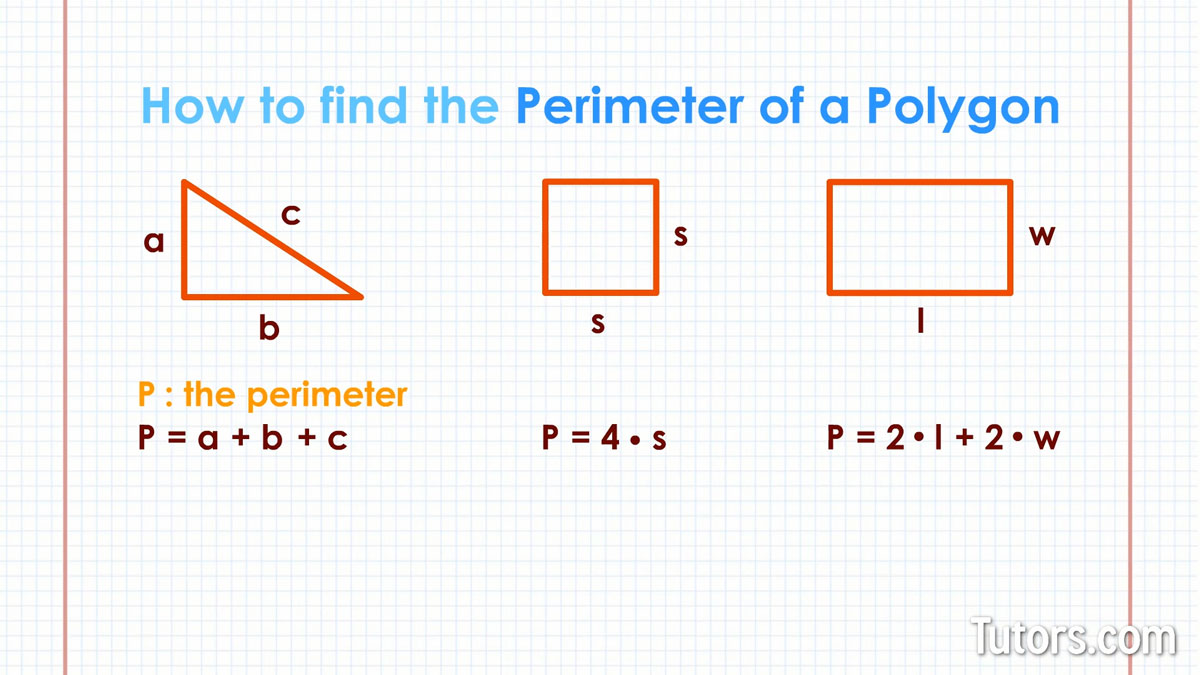
For most shapes, especially polygons, finding the perimeter is quite simple, actually. You just add up the lengths of all its sides. My text states, "In the figure below, the perimeter of each shape is the sum of the lengths of each side." This is the core principle, you know. If you can measure each side, you can find the perimeter, which is pretty much it.
- Punta Cana Missing Girl
- Caitlin Clark Rookie Card
- How To Erase Gel Nail Polish
- Taper Fade Black Men
- How Many Children Does Pam Bondi Have
Say, for example, we have a triangle, as my text suggests. A triangle, obviously, has three sides. To find its perimeter, you simply measure the length of each of those three sides and then add those measurements together. It's that straightforward, more or less. This method works for any polygon, no matter how many sides it has, which is very convenient.
Even for irregular shapes, the process stays the same. You just need to determine the length of all the sides of the given figure and then mark them, as my text advises. Once you have all those individual lengths, you simply combine them through addition. This is, you know, the most basic and universal method for finding perimeter, and it's rather effective.
Finding Perimeter for Common Shapes
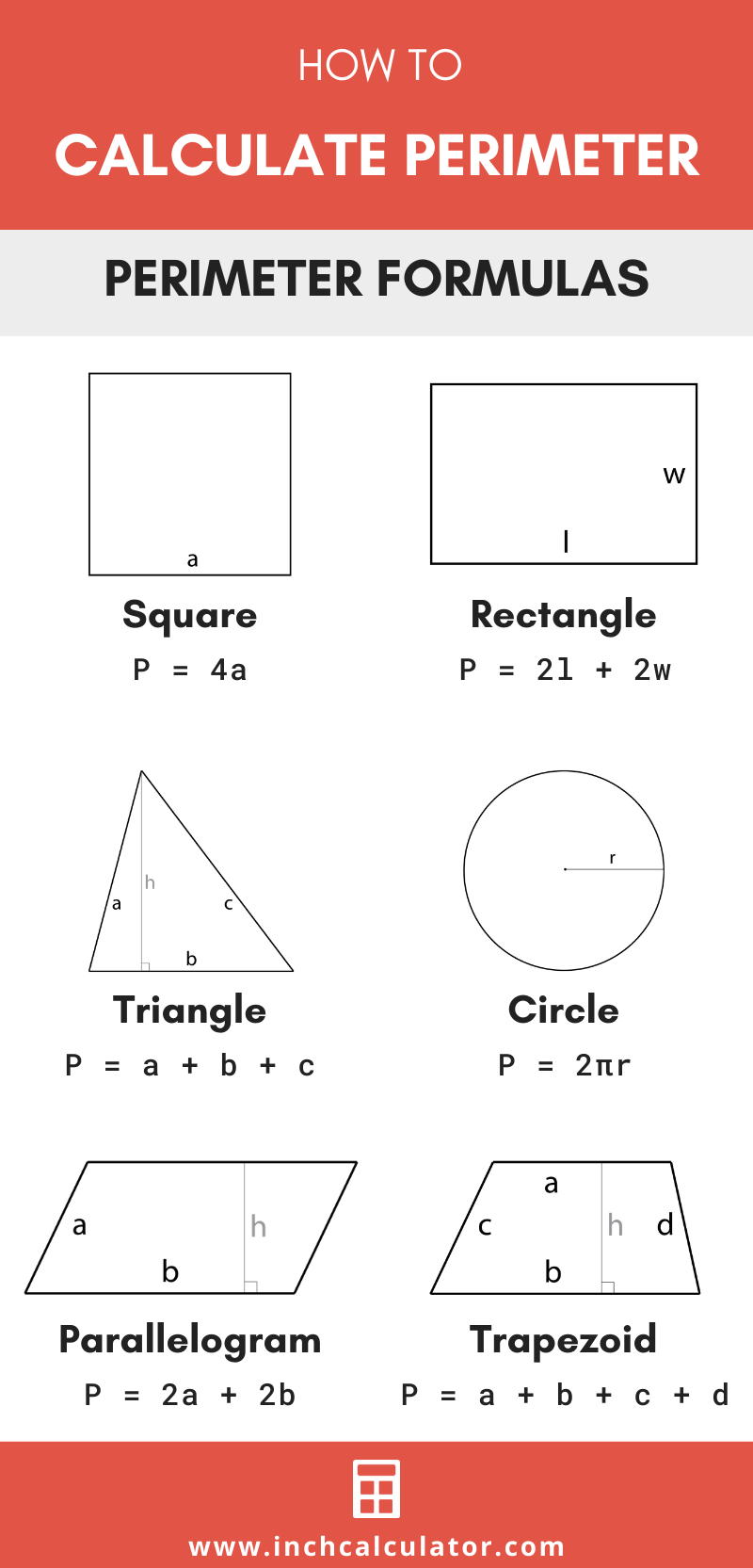
While the "add all sides" rule works for everything, some common shapes have specific formulas that can make the calculation even quicker, which is rather helpful. My text mentions perimeter formulas for various shapes, including squares, rectangles, and triangles. Let's look at a few of these, because they're quite common, you know.
Squares: All Sides Equal
A square is a special kind of rectangle where all four sides are exactly the same length, which is a key characteristic. So, if one side of a square measures 5 units, every other side also measures 5 units, you know. Instead of adding 5 + 5 + 5 + 5, which works perfectly fine, there's a quicker way, actually.
The formula for the perimeter of a square is simply: Perimeter = 4 × side length. This is because you have four equal sides, so multiplying the length of one side by four gives you the total distance around, which is very efficient. For instance, a square with a side of 7 inches would have a perimeter of 4 × 7 = 28 inches, you know, which is quite easy to figure out.
Rectangles: Two Pairs of Equal Sides
Rectangles have four sides, but unlike squares, only opposite sides are equal in length, which is a distinct feature. They have a length and a width, as my text mentions. So, if you have a rectangle, the top side is the same length as the bottom side, and the left side is the same length as the right side, you know.
My text explains, "To calculate the perimeter, add twice the length to twice the width." This gives us the formula: Perimeter = 2 × (length + width) or Perimeter = (2 × length) + (2 × width). Both forms essentially mean the same thing, actually, which is quite useful. So, if a rectangle is 10 feet long and 5 feet wide, its perimeter would be (2 × 10) + (2 × 5) = 20 + 10 = 30 feet, which is pretty straightforward.
On a rectangle, for instance, the perimeter is the total length of the rectangle's outline, including all its sides, you know, as my text points out. This formula helps you find that total distance quickly, without having to measure each side individually if you already know the length and width, which is a rather handy shortcut.
Triangles: Three Sides to Add
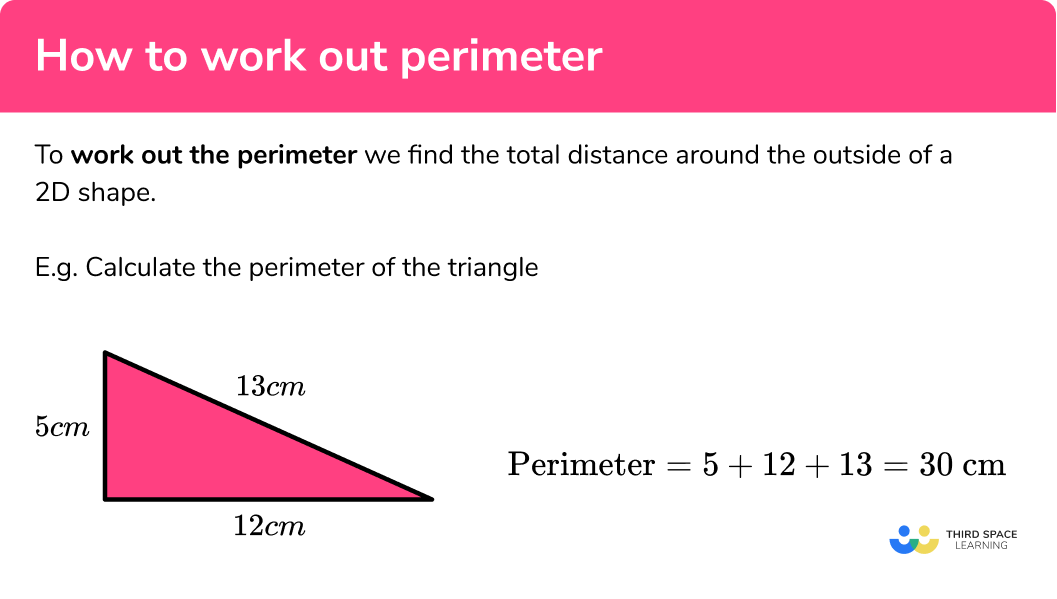
As my text briefly mentions, a triangle has three sides. Finding its perimeter is a classic example of the basic "add all sides" rule, you know. There isn't a special multiplication formula unless it's an equilateral triangle (where all three sides are equal), but even then, just adding them works just fine, actually.
So, if you have a triangle with sides measuring 3 cm, 4 cm, and 5 cm, you just add them up: 3 + 4 + 5 = 12 cm. That's its perimeter, in a way. It's really that simple, which is rather reassuring for anyone learning this concept, you know. My text says, "The number of sides a triangle has is 3," which reinforces this basic understanding.
Irregular Shapes: Still Just Adding
Sometimes, shapes aren't neat squares or rectangles. They might have many sides, and those sides might all be different lengths, you know. These are what we call irregular shapes. But don't let the word "irregular" make you think it's complicated; it's not, actually. The process for finding their perimeter is exactly the same as the basic rule we discussed.
You simply measure each individual side of the irregular shape and then add all those measurements together, in a way. My text says, "Learn how to find the perimeter of regular & irregular shapes." The key is to make sure you measure every single side and don't miss any, which is rather important. If you have a shape with seven sides, you'll add seven numbers, which is pretty much it.
For example, imagine a shape that looks like an L. It might have sides of 4 units, 2 units, 1 unit, 3 units, 3 units, and 5 units. To find its perimeter, you would add 4 + 2 + 1 + 3 + 3 + 5, which equals 18 units, you know. It's just careful addition, actually, and that's all there is to it.
Other Polygons: The Same Simple Rule
My text notes, "The perimeter of a polygon is the distance around the outside of the polygon." Polygons are simply closed shapes made up of straight line segments, you know. This includes everything from pentagons (5 sides) and hexagons (6 sides) to octagons (8 sides) and shapes with even more sides. For all of them, the fundamental rule applies, which is pretty consistent.
If a polygon is "regular," meaning all its sides are the same length, you can use a shortcut: multiply the length of one side by the number of sides, in a way. For instance, a regular hexagon with sides of 6 cm would have a perimeter of 6 × 6 = 36 cm, you know. But if the polygon is irregular, you just go back to adding each side individually, which works every time, actually.
This lesson will show that finding the perimeter of regular or irregular polygons, it is a very straightforward process, as my text points out. You just need to be able to identify all the sides and measure them accurately, and that's pretty much it for all these shapes, you know.
Tackling Perimeter Word Problems
Perimeter word problems are just practical situations described in words, where you need to find the distance around something, you know. My text mentions, "We will also look at perimeter word problems." These problems often ask you to apply the perimeter concept to real-world scenarios, which is rather useful for understanding its application.
For example, a problem might say: "A rectangular garden is 15 meters long and 8 meters wide. How much fencing is needed to go around it?" Here, you need to find the perimeter of the garden, which is a rectangle, actually. Using the formula (2 × length) + (2 × width), you'd calculate (2 × 15) + (2 × 8) = 30 + 16 = 46 meters of fencing, you know. It's just applying the formula to a story.
Another example could be: "Sarah wants to put a decorative border around a triangular picture frame. The sides of the frame measure 20 cm, 25 cm, and 30 cm. What is the total length of the border she needs?" Here, you'd add the three sides: 20 + 25 + 30 = 75 cm, you know. These problems test your ability to read carefully and then apply the correct perimeter method, which is pretty much it.
The key to solving these is to first determine the shape you want to measure, as my text advises. Then, identify the given side lengths or the information needed to find them, in a way. Finally, apply the appropriate formula or simply add all the side lengths. It's a logical step-by-step process, which is very helpful.
Why Does Knowing Perimeter Matter?
Understanding how to find perimeter isn't just a math class exercise; it has many practical uses in daily life, actually. For instance, if you're planning to put up a fence around your yard, you'll need to know the perimeter to buy the right amount of fencing material, you know. Or, if you're putting trim around a room, you need to measure the perimeter to know how much trim to purchase, which is rather important.
My text highlights the utility of learning the definition and different methods to find the perimeter, followed by formulas for different shapes, comparisons, and uses. It's a skill that comes in handy for home improvement projects, crafting, designing, and even in professional fields like architecture or construction, you know. Knowing this helps you estimate materials and costs, which is pretty much essential.
It helps you visualize and plan spaces effectively, too. If you're designing a small garden bed, knowing its perimeter helps you decide how many edging stones you'll need, in a way. It's a foundational skill that supports many other calculations and real-world applications, which is why it's so widely taught and used, you know.
For more insights into basic geometric concepts, you might find resources like Khan Academy's Geometry section very helpful, as they often explain things in a way that builds on these fundamental ideas, which is rather good. You can also learn more about shapes and measurements on our site, and link to this page for a comparison of area and perimeter.
Common Questions About Perimeter
People often have a few common questions when they're trying to figure out how to find perimeter, you know. Let's address some of those that come up rather frequently, actually, to help clear things up even more.
What is the difference between perimeter and area?
This is a very common question, you know. Perimeter is the distance around the outside of a shape, like the length of a fence. Area, on the other hand, is the amount of surface inside the shape, like the grass within that fence. My text mentions, "Multiply the length by the width to get the area of a shape," which highlights this difference. So, perimeter is about the boundary, and area is about the space it covers, which is pretty much it.
Can you find the perimeter of a circle?
Yes, you can, actually, but it has a special name and a different formula, you know. The perimeter of a circle is called its circumference. Instead of adding sides, you use the formula Circumference = π × diameter, or 2 × π × radius. My text does mention "circles" in its list of shapes, so it's good to know this distinction, which is rather important for round shapes.
Is perimeter always measured in units of length?
Yes, absolutely, you know. Perimeter is always a measure of length. So, it's measured in units like centimeters, meters, inches, feet, or miles, depending on the size of the shape. It's a one-dimensional measurement, representing distance, which is pretty consistent across all shapes and situations, actually. This is a key point to remember when stating your answer, which is rather vital.
So, as you can see, learning how to find the perimeter of various shapes with our comprehensive guide has hopefully made this concept much clearer for you. We've explained the basics of perimeter, provided clear examples for rectangles, squares, and irregular shapes, and, you know, shown that it's a very practical skill for many parts of life, which is rather useful to know today, on this day, October 26, 2023.
- Steve Horstmeyer Dogs
- Eminence In Shadow Season 3
- Nagi Hikaru
- Blowout Taper Straight Hair
- Business Class Vs First Class
Perimeter Formula
How To Find The Perimeter Of A Rectangular Painting at Lisa Rubino blog
Finding Perimeter