How To Turn A Decimal Into A Fraction: Your Easy Guide

Myles King 20 Aug 2025

Unlocking the Power of Fractions from Decimals
Why Bother Converting Decimals to Fractions?
The Simple Three-Step Process: Read, Write, Reduce
Putting it into Practice: Examples
Handling Decimals with Whole Number Parts (Mixed Numbers)
What About Repeating Decimals?
Handy Tools: Calculators and Online Converters
Frequently Asked Questions About Decimal to Fraction Conversion

Have you ever looked at a decimal number and wished you could just turn it into a fraction, maybe for a recipe, a school assignment, or just to make sense of some measurements? Well, you're certainly not alone. Turning decimals into fractions is a widespread activity we carry out in our daily lives, even if we don't always realize it.

It might seem a bit tricky at first, a little like trying to speak a different language, but honestly, converting a decimal to a fraction isn't as hard as it looks. With just a few simple steps, you can actually transform those decimal numbers into neat, tidy fractions without much fuss. It's truly a skill that comes in handy, you know, more often than you might think.

This article will guide you through the process of converting decimals into fractions, showing you a straightforward method that makes it pretty simple. We'll walk through each step together, so you can feel really confident in your ability to make these conversions at the drop of a hat. So, let's get started, shall we, and make sense of those numbers!

Why Bother Converting Decimals to Fractions?

You might wonder why we even need to change decimals into fractions. After all, decimals seem pretty straightforward for things like money or digital measurements. But, as a matter of fact, fractions offer a different kind of precision and can be much easier to work with in certain situations, especially when you're dealing with parts of a whole.

Think about cooking, for instance. A recipe might call for "three-quarters of a cup" rather than "0.75 cups." Or, say you're building something and need to cut a piece of wood that's exactly "one-eighth of an inch" thick. Fractions help us visualize and divide things into equal parts more intuitively. They really do, in a way, give us a clearer picture of proportions.

Sometimes, too it's almost, fractions are just more exact. When a decimal goes on forever, like 0.3333..., converting it to a fraction like 1/3 gives you the exact value without needing to round anything. This kind of accuracy is actually quite important in many areas, from science to engineering, and even just in making sure your measurements are spot on. It's a pretty useful skill to have, to be honest.

The Simple Three-Step Process: Read, Write, Reduce

Good news! Changing a decimal to a fraction can be broken down into just three easy steps. My text mentions a method that is quite effective: "Read — write — reduce." This approach helps us systematically transform any decimal into its fractional counterpart. It’s a pretty logical flow, and once you get the hang of it, you’ll find it quite intuitive, you know.

We'll go through each of these steps in detail, using examples to show you just how they work. The key is to pay attention to the decimal's place value, which is actually the biggest helper in this whole process. So, let's unpack these steps and see how they can make your number conversions much simpler, basically.

Step 1: Read the Decimal Aloud (Understand its Place Value)

This first step is arguably the most important because it helps you figure out the denominator of your fraction. When you read a decimal aloud, you're essentially stating its value in terms of tenths, hundredths, thousandths, and so on. For instance, 0.5 is "five tenths," and 0.25 is "twenty-five hundredths."

The last digit of your decimal tells you its place value. If the last digit is in the tenths place, your fraction will be over 10. If it's in the hundredths place, it will be over 100, and if it's in the thousandths place, it will be over 1000. It's pretty straightforward, really. This understanding forms the foundation for the next step, as a matter of fact.

For example, if you have 0.7, the 7 is in the tenths place, so you'd say "seven tenths." If you have 0.12, the 2 is in the hundredths place, so you'd say "twelve hundredths." This simple act of reading it out loud actually helps you see the fraction hiding within the decimal. It’s a pretty neat trick, honestly.

Step 2: Write it as a Fraction Over a Power of 10

Once you've read the decimal and identified its place value, the next step is to write it as a fraction. My text suggests, "Create a fraction by putting the decimal over 1," or "Write the decimal divided by one." This is your starting point. For example, say you’re given the decimal .55, your first step is to write out the decimal so it looks like .55 / 1.

Now, to get rid of the decimal point in the numerator, you need to multiply both the top (numerator) and the bottom (denominator) by a power of 10. You multiply by 10 for every number after the decimal point. So, if there's one digit after the decimal, you multiply by 10. If there are two digits, you multiply by 100, and if there are three, you multiply by 1000, and so on.

Let's use our .55 example. Since there are two digits after the decimal point (the 5 and another 5), you'd multiply both the numerator and the denominator by 100. So, (.55 / 1) becomes (0.55 * 100) / (1 * 100), which gives you 55 / 100. This process effectively moves the decimal point to the right, giving you a whole number in the numerator, you know.

Step 3: Reduce the Fraction to its Simplest Form

The final step is to simplify, or reduce, the fraction you've created. This means finding the largest number that can divide evenly into both the numerator and the denominator. This number is called the greatest common factor (GCF). Dividing both parts of the fraction by their GCF gives you the fraction in its simplest, most elegant form.

For example, if you have the fraction 55/100, you need to find a number that divides both 55 and 100. You might notice that both numbers end in 0 or 5, which means they are both divisible by 5. So, you divide 55 by 5 (which is 11) and 100 by 5 (which is 20). This gives you the simplified fraction 11/20.

Sometimes, you might need to divide by common factors more than once if you don't find the GCF right away. Just keep dividing until the only common factor between the numerator and denominator is 1. This ensures your fraction is as simple as it can possibly be, and it’s actually a pretty satisfying part of the process, too.

Putting it into Practice: Examples

Let's walk through a few examples to really solidify these steps. Seeing them in action often makes the whole process much clearer, you know. We'll use the "Read, Write, Reduce" method for each one. This way, you can get a good feel for how it works with different types of decimals, basically.

Example: Converting 0.55 to a Fraction

This is a great example from my text, so let's use it. We want to convert 0.55 into a fraction. It's a pretty common kind of decimal you might see.

Step 1: Read
We read 0.55 as "fifty-five hundredths." The last digit, 5, is in the hundredths place.
Step 2: Write
Since it's "fifty-five hundredths," we write it as 55 over 100. So, we have 55/100. This is the fraction form before simplifying, you know.
Step 3: Reduce
Now, we look for a common factor for 55 and 100. Both numbers are divisible by 5.
55 ÷ 5 = 11
100 ÷ 5 = 20
So, 55/100 simplifies to 11/20.
And there you have it! 0.55 is the same as 11/20. Pretty neat, right?

Example: Converting 0.25 to a Fraction

Here's another common decimal. Let's try 0.25. This one is actually quite familiar to many people, especially when thinking about money, like a quarter, you know.

Step 1: Read
We read 0.25 as "twenty-five hundredths." The last digit, 5, sits in the hundredths place.
Step 2: Write
Because it's "twenty-five hundredths," we write it as 25 over 100. So, our fraction is 25/100.
Step 3: Reduce
Now, we find a common factor for 25 and 100. Both are clearly divisible by 25.
25 ÷ 25 = 1
100 ÷ 25 = 4
So, 25/100 simplifies to 1/4.
This shows that 0.25 is indeed equivalent to 1/4, which makes a lot of sense, especially with money, as a matter of fact.

Example: Converting 0.125 to a Fraction

Let's try one with three decimal places: 0.125. This might seem a little more involved, but the steps are essentially the same, you know. It’s just a slightly larger power of ten, basically.

Step 1: Read
We read 0.125 as "one hundred twenty-five thousandths." The last digit, 5, is in the thousandths place.
Step 2: Write
Since it's "one hundred twenty-five thousandths," we write it as 125 over 1000. So, our fraction is 125/1000.
Step 3: Reduce
Finding the GCF for 125 and 1000 might take a couple of steps, or you might spot that both are divisible by 25. Let's try 25 first.
125 ÷ 25 = 5
1000 ÷ 25 = 40
Now we have 5/40. We can reduce this further, as both 5 and 40 are divisible by 5.
5 ÷ 5 = 1
40 ÷ 5 = 8
So, 125/1000 simplifies to 1/8.
This means 0.125 is exactly 1/8. It’s pretty satisfying when you get to the simplest form, honestly.

Handling Decimals with Whole Number Parts (Mixed Numbers)

What if your decimal has a whole number part, like 3.75? My text mentions that "Now it’s time to look at a decimal that has both a whole number part and a decimal part." This is where we create what's called a mixed number. It's actually not much harder, you know.

The whole number part simply stays as a whole number. You just focus on converting the decimal part into a fraction using the "Read, Write, Reduce" steps we just covered. Then, you put the whole number and the fraction together.

For example, with 3.75:

The whole number is 3. Keep that aside for a moment.
Now, look at the decimal part: 0.75.
Convert 0.75 to a fraction:
- Read: "seventy-five hundredths."
- Write: 75/100.
- Reduce: Both 75 and 100 are divisible by 25. 75 ÷ 25 = 3, and 100 ÷ 25 = 4. So, 0.75 becomes 3/4.
Put the whole number back with the fraction: 3 and 3/4.

So, 3.75 as a mixed number is 3 3/4. It's essentially two separate conversions that you just combine, which is pretty straightforward, really.

What About Repeating Decimals?

Repeating decimals are those numbers that have a pattern of digits that goes on forever, like 0.333... or 0.141414... Converting these manually can be a bit more involved than with terminating decimals. My text points out, "For repeating decimals enter how many decimal places in your decimal number." This is often a hint that a calculator or a specific method is preferred.

While there are manual algebraic methods to convert repeating decimals to fractions (like setting x equal to the decimal and multiplying by powers of 10 to subtract and solve), they can be a bit complex for a quick conversion. For instance, 0.333... becomes 1/3. And 0.141414... becomes 14/99.

However, with the help of a calculator, converting decimals into fractions can become an easy and efficient task, especially for repeating ones. Many scientific calculators and online tools are actually designed to handle these types of conversions instantly. It's often the simplest way to get the job done accurately and quickly, you know.

Handy Tools: Calculators and Online Converters

While knowing the manual steps is incredibly useful and builds a solid foundation, there are certainly times when you might want a quicker way. My text mentions, "This calculator converts a decimal number to a fraction or a decimal number to a mixed number." It also says, "You can use this online decimal to fraction converter to convert a given decimal into a fraction instantly without any calculation."

These tools are incredibly helpful, particularly when you're dealing with very long decimals or repeating decimals where manual calculation might be prone to errors or just take too much time. An online converter, for instance, typically just asks you to type in your decimal, and then it provides the fraction in its simplest form right away. It's pretty much instant, you know.

Using these converters can be a real time-saver, especially if you're checking your work or if you just need a quick answer. They ensure accuracy and efficiency, making what could be a slightly tedious task into something that's really quite simple. Learn more about fractions and decimals on our site, and for a practical tool, you can often find a good decimal to fraction calculator online to help with these conversions.

Frequently Asked Questions About Decimal to Fraction Conversion

How do you convert 0.5 to a fraction?

To convert 0.5 to a fraction, you follow the three steps: Read, Write, Reduce. First, you read 0.5 as "five tenths." This tells you to write it as 5/10. Then, you reduce the fraction by finding a common factor for 5 and 10, which is 5. Dividing both by 5 gives you 1/2. So, 0.5 is 1/2. It's pretty straightforward, really.

What is the easiest way to convert a decimal to a fraction?

The easiest way to convert a decimal to a fraction depends on the decimal. For simple, terminating decimals, the "Read, Write, Reduce" method is actually quite easy and fast once you've practiced it a bit. You just say the decimal aloud to find its place value, write it as a fraction over a power of 10, and then simplify. For more complex or repeating decimals, using an online decimal to fraction converter or a calculator is often the most efficient and easiest approach, as a matter of fact. They handle the calculations instantly.

How do you convert a repeating decimal to a fraction?

Converting a repeating decimal to a fraction manually involves a few more steps than with a terminating decimal. For instance, for 0.333..., you would set x = 0.333..., then multiply by 10 to get 10x = 3.333.... Subtracting the first equation from the second gives you 9x = 3, so x = 3/9, which simplifies to 1/3. However, my text suggests that for repeating decimals, you often "enter how many decimal places in your decimal number" into a calculator. This implies that using a specialized calculator or an online converter is generally the easiest and most reliable way to convert repeating decimals into fractions, saving you from the manual algebraic steps. It's a pretty handy shortcut, you know.

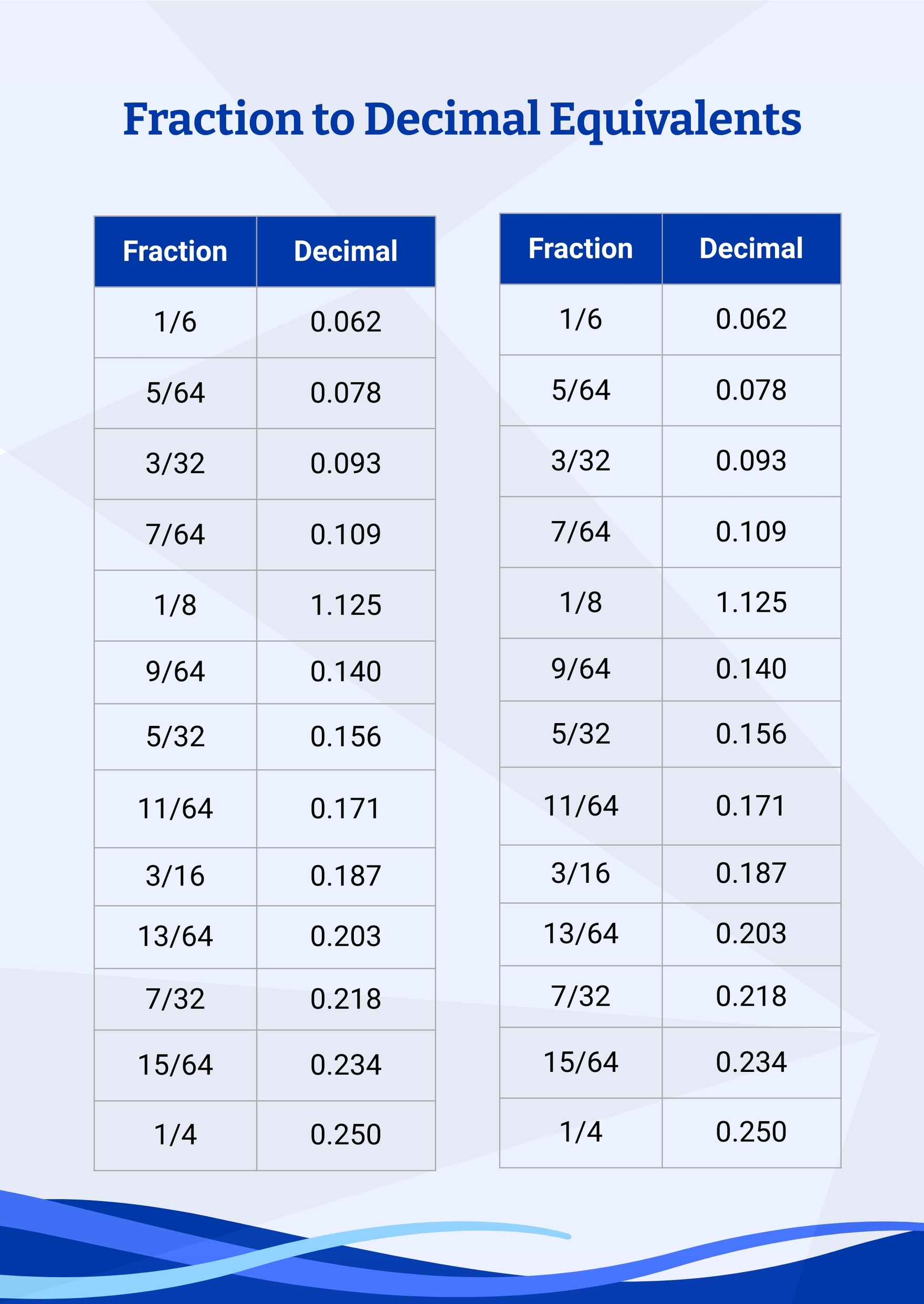
Fraction-decimal Chart in Illustrator, PDF - Download | Template.net

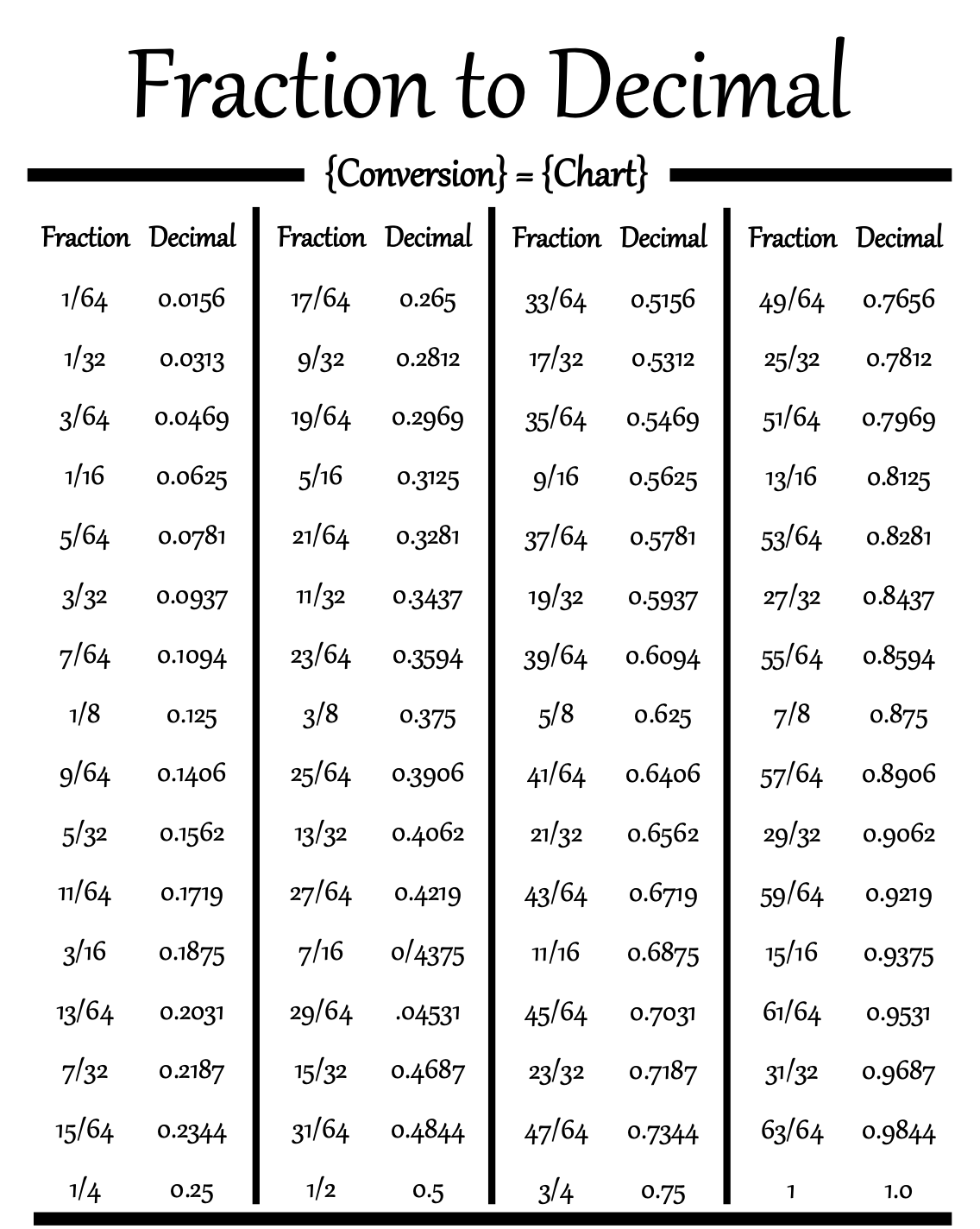
Decimal To Fraction Chart Cuemath - TimeChart.net

Decimal to Fraction: 3 Easy Steps — Mashup Math

Celeflash News