What Is Range In Math: Uncovering The Spread Of Numbers
Have you ever looked at a bunch of numbers and wondered just how spread out they are? Well, that, you know, is where the idea of range comes in very handy. It's a way we can get a quick sense of how much difference there is between the biggest and smallest items in any collection of figures. This simple concept, actually, helps us understand data better, whether we are talking about test scores or daily temperatures.
Understanding what range is in math helps us see the bigger picture of a data set. It's not just about knowing the average or the middle value; it’s about grasping the full extent of the numbers you are looking at. This basic measure, so, provides a really quick snapshot of variation, giving us a useful initial insight into any group of numbers we might be studying.
In this guide, we'll explore what range truly means, how you find it for different kinds of number groups, and why it's a helpful tool in both statistics and functions. We will, of course, look at how it helps us make sense of the world around us, from understanding prices to knowing about heights. Let's get into it, shall we?
- Kimberly Guilfoyle Before And After
- Shasha Prasad
- Burger King Crown Guy
- What Is A Torta
- How To See Deleted Sms
Table of Contents
- What is Range? A Simple Explanation
- Range in Statistics: Finding the Spread of Data
- Range in Functions: The Output Values
- Why is Range Important in Math?
- Range Compared to Other Measures: Mean, Median, Mode
- Frequently Asked Questions About Range
- Bringing It All Together: The Power of Range
What is Range? A Simple Explanation
At its very core, the range in math refers to the difference between the largest and smallest values in a set of numbers. Think of it, you know, as the spread of your data. It shows how far apart the values are from each other. This is a pretty straightforward idea, giving us a quick way to see how much variation exists within a group of figures.
In mathematics, the term 'range' tells us how spread out numbers are in a set of data. It's the difference between the largest and smallest values in a group of numbers, actually. This simple yet powerful way helps us understand the spread or dispersion of data, which is quite useful for many things. It really just gives us a sense of how wide the net of numbers is.
The range of a collection of numbers is the distance between the largest and smallest numbers in the collection. We subtract the smallest value from the biggest value to determine a set's range, in a way. This calculation, you see, is a fundamental component of every data collection and helps us grasp the extent of the data points involved.
Range in Statistics: Finding the Spread of Data
When we talk about range in statistics, we are usually looking at a group of numbers, like survey results or temperature readings. Here, the range is the interval between the two extremes—the highest and lowest values—of the distributed numbers. It is, you know, a crucial component of every data collection because it offers an immediate glimpse into the variability.
In statistical concepts, range is used to understand the spread of data. It is calculated by subtracting the lower value from the upper value in a dataset, which is pretty simple. This helps us get an insight into the overall dispersion of the numbers, giving a quick idea of how widely scattered they might be. It's a very direct way to see the boundaries of your information.
How to Calculate Range for a Data Set
Calculating the range for a data set is really quite simple. You just need to follow a couple of steps. First, you find the highest value in your set of numbers. Then, you find the lowest value in that same set. Finally, you subtract the lowest value from the highest value. That difference, you know, is your range.
For example, if you have a list of numbers like 5, 12, 3, 18, 7, you would first spot the largest number, which is 18. Then, you'd find the smallest number, which is 3. To get the range, you'd do 18 minus 3, which gives you 15. So, the range for that set of numbers is 15. It's a very straightforward calculation, as a matter of fact.
The formula for range in statistics is: Range = Highest Value - Lowest Value. This simple formula, you see, helps us quickly grasp the extent of the data's spread. It's a fundamental concept that applies across various fields, providing insight and clarity on the variability within a dataset. It's something you will use quite often, actually.
Examples of Range in Statistics
Let's look at some everyday examples to see how range works. Suppose you have a list of daily high temperatures for a week: 70, 75, 68, 80, 72, 78, 71 degrees Fahrenheit. The highest temperature here is 80 degrees, and the lowest is 68 degrees. So, the range for these temperatures would be 80 - 68 = 12 degrees. This tells you the temperature varied by 12 degrees over that week, which is quite a bit.
Consider another example with student test scores: 65, 88, 72, 95, 78, 81. The highest score is 95, and the lowest score is 65. The range for these scores is 95 - 65 = 30. This means there's a 30-point difference between the best and worst scores, giving you a sense of how varied the student performance was. It's a quick way to see the spread, you know.
Or, what about prices of a certain item at different stores: $15, $12, $18, $14, $16? The highest price is $18, and the lowest is $12. The range is $18 - $12 = $6. This tells you that the price of that item can vary by $6 from one store to another, which could be useful information for shoppers, you see. It really helps to compare things quickly.
Range in Functions: The Output Values
The term 'range' has different meanings in statistics and mathematics, as a matter of fact. While in statistics it's about the difference between the highest and lowest values, in functions, it takes on a slightly different role. Here, the range refers to the set of all possible output values that a function can produce. It's about what comes out, you know, after you put something in.
When we talk about the range of a function, we are thinking about all the results you could get. A domain is all the values that can go into a function for which it gives a valid output. It is the set of all the possible inputs. The range, then, is the set of all the possible outputs that correspond to those inputs. It's really about the results, you see, of the function's work.
Understanding Function Outputs
Imagine a function as a machine. You put something in (an input from the domain), and the machine does something to it, then spits something out (an output). The range of that function is every single possible thing that machine could ever spit out, no matter what valid input you give it. It's the complete collection of all the answers the function can give, so to speak.
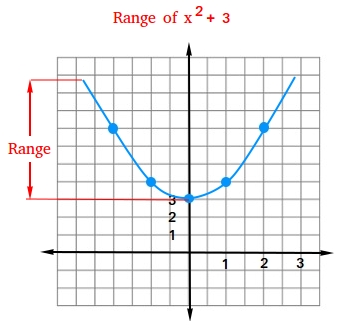
For example, if you have a function that squares every number you give it, like f(x) = x². If you put in any real number, the output will always be zero or a positive number. You can't get a negative number by squaring a real number. So, the range of this function, in a way, would be all non-negative real numbers. This means the outputs will always be 0 or higher, you know.
It's important to distinguish this from the statistical range. In functions, we're not subtracting values; we're listing or describing all the possible outcomes. It's a set of values, not a single number representing a difference. This distinction, actually, is quite important when you are learning about different mathematical ideas. It's a different kind of "spread," you might say.
How to Find the Range of a Function
Finding the range of a function can sometimes be a bit more involved than finding the range of a data set. It often requires looking at the graph of the function or using algebra to figure out what values the output (usually represented by 'y' or f(x)) can take. You are essentially asking: what are all the possible 'y' values that this function can produce? This can take a little thought, you know.
For simple functions, you might just think about what happens when you plug in different numbers. For f(x) = x + 2, if you can put in any real number, then you can get out any real number. So the range, in this case, would be all real numbers. It's a direct relationship, so, the outputs mirror the inputs pretty closely.
For more complex functions, you might need to consider things like square roots (which can't have negative numbers inside if we are dealing with real numbers) or fractions (where the denominator can't be zero). These restrictions on the input, you know, often affect what outputs are possible, thus shaping the function's range. Graphing the function can also really help you visualize the range, as a matter of fact.
Why is Range Important in Math?
The range is a fundamental concept that applies across various fields, providing insight and clarity on the spread of data. It's a simple measure, yes, but its importance can't be overstated. It gives us a quick and easy way to understand the variability within a set of numbers, which is pretty useful for making initial observations. This quick glance, you know, can often guide further analysis.
In statistical analysis, the range is used to understand the spread of data. It helps get an insight into the overall distribution. For example, if you're looking at product prices, a small range means prices are pretty consistent, while a large range suggests a lot of variation. This information, you see, can be very helpful for businesses or consumers trying to make decisions.
The range of a data set is the difference between its highest and lowest values, while the range of a function is the set of all possible output values. Both meanings, though different, are vital for understanding the scope of numbers involved in a particular mathematical context. They help define the boundaries, you know, of what you are working with.
Advantages of Using Range
One of the biggest advantages of range is its simplicity. It's really easy to calculate and understand, even for someone who is not deeply familiar with statistics. You just need two numbers: the highest and the lowest. This makes it a very accessible tool for a quick assessment of data spread. It's a straightforward measure, you know, that anyone can grasp.
It provides a clear picture of the overall spread of the data. If you're comparing two different groups of numbers, seeing their ranges side-by-side can give you an immediate sense of which group has more variation. This quick comparison, you see, is often the first step in any data analysis. It helps to set the stage for deeper insights.
The range is a crucial component of every data collection because it helps us quickly understand the distance between the largest and smallest numbers. This immediate feedback about the data's boundaries can be very valuable in many situations, from scientific experiments to everyday decision-making. It's a really good starting point, as a matter of fact, for any data exploration.
Limitations to Keep in Mind
While range is simple and useful, it does have some limitations. Because it only uses the highest and lowest values, it can be heavily affected by outliers. An outlier is a number that is much higher or much lower than the rest of the data. Just one extreme value, you know, can make the range seem much larger than the actual spread of most of the data.
For example, if most test scores are between 70 and 90, but one student scores a 10, the range would be 90 - 10 = 80. This 80-point range might suggest a huge spread in scores, even though most students were fairly close. The single low score, you see, distorts the picture of the typical student performance. This is something to really consider.
The range also doesn't tell you anything about how the numbers are distributed between the highest and lowest points. Are they all clustered near one end, or are they evenly spread out? The range alone won't tell you this. For a more complete picture of data spread, you might need to look at other statistical measures, which we will touch on briefly. It's a good first step, but not the whole story, you know.
Range Compared to Other Measures: Mean, Median, Mode
The range is just one way to describe a set of numbers. Other common measures include the mean, median, and mode. Each of these gives us a different piece of information about the data. The mean is the numerical average, found by adding all the numbers and dividing by how many there are. The median is the exact middle value when the numbers are arranged in order. The mode is the number that appears most often in the set. These measures, you know, all work together to paint a full picture.
In statistical analysis, the range is the lowest to highest score. The median is the exact middle, and the mean is the numerical average. Each of these measures helps us understand different aspects of the data. For instance, the mean gives you a sense of the "typical" value, while the median helps if there are extreme values that might skew the average. The range, then, tells you the full breadth of the data, which is quite useful.
Knowing all these measures helps you get a well-rounded view of your data. The range quickly shows you the extent of the numbers, while the mean, median, and mode give you insights into the central tendency or the most common values. They are all tools in your mathematical toolbox, you see, and each has its own purpose. To really understand a dataset, you often need to look at more than just one of these.
You can learn more about central tendency measures on our site, which helps explain how mean, median, and mode fit into this bigger picture. It's all about understanding different ways to look at numbers. For more specific examples on calculating these, you can also check out this page our guide to data analysis basics, which goes into more detail, as a matter of fact.
Frequently Asked Questions About Range
People often have questions about what range is in math, so let's clear up some common ones.
What is the main difference between range in statistics and range in functions?
Basically, in statistics, range is a single number that tells you the difference between the highest and lowest values in a data set. It's about the spread of specific numbers you have. In functions, however, range refers to the entire set of all possible output values the function can produce. It's a collection of results, not a single difference, you know. They are both about "spread" but in different ways.
Can the range ever be zero?
Yes, the range can definitely be zero! This happens when all the numbers in your data set are exactly the same. For example, if your data set is {5, 5, 5, 5}, the highest value is 5 and the lowest value is 5. So, 5 - 5 = 0. A range of zero means there is no variation at all in your numbers, which is pretty straightforward. It means everything is identical, actually.
Why is it important to know the range along with the mean or median?
Knowing the range along with the mean or median gives you a much better overall picture of your data. The mean or median tells you about the "center" of your data, but they don't tell you anything about how spread out the numbers are. The range, you see, fills that gap by showing you the total spread from the smallest to the largest value. This combination helps you avoid misleading conclusions that might come from looking at just one measure. For example, two datasets might have the same mean, but very different ranges, which is quite important to understand.
Bringing It All Together: The Power of Range
So, you see, range is a pretty straightforward yet powerful concept in math. Whether you are looking at a set of numbers in statistics or understanding the possible outputs of a function, the idea of range helps us grasp the extent and variability of values. It's a quick way to measure the distance between the smallest and largest values, giving us a really useful first impression of any data we encounter. This simple calculation, as a matter of fact, provides a foundational insight into data distribution.
From understanding the spread of heights in a group to the possible outcomes of a mathematical model, range provides a clear picture. It helps us make sense of the world by giving us a direct measure of how much things can vary. Keep practicing with different examples, and you'll find that using range becomes second nature. It's a skill that will serve you well in many areas of life, you know, helping you interpret numbers with greater confidence.
For further reading and to deepen your understanding of these concepts, you might find resources like Khan Academy's explanation of measures of spread quite helpful. They often have very clear explanations and practice problems. It's always a good idea to explore different perspectives to really solidify your knowledge, which is quite true for any learning journey.
- Help I Accidentally Summoned Mahoraga
- Deep Winter Color Palette
- Can You Eat Crocs
- Space City Home Network
- How Did Mr Beast Get Rich
Range of a Function

The Range (Statistics)

4 Ways to Find the Range of a Function in Math - wikiHow