Mastering Decimal To Fraction Conversion: Your Guide To Precision Numbers
Have you ever looked at a decimal number, like 0.14, and wondered how you could change it into a neat fraction, say 7/50? Many people, it turns out, really want to grasp how to convert decimals to fractions. This skill is actually quite useful, whether you are balancing a budget, working on a school assignment, or even writing code. It brings a lot more clarity and precision to your numbers, which is often a better choice than using those sometimes-tricky floating-point values that can be a bit imprecise, as my text points out.
You see, when you are working with numbers, especially in areas where exactness truly counts, decimals can sometimes give you a slightly "off" answer. This is because some fractions, like 1/3, do not have a perfectly neat decimal representation; they go on and on. So, understanding how to convert decimals to fractions helps you keep things exact, preventing those "weird" fractions that might pop up from imprecise calculations, which is something many folks want to avoid, you know?
This guide is here to show you a simple way to change those decimal numbers into their fractional forms. We will cover both decimals that stop and those that repeat forever. We will also touch on why this is so important for accuracy, and how you can even get a bit more control over how those fractions look, perhaps by limiting their bottom number, so it's all a bit clearer.
- What Happened To Jessica Tarlov
- Is Clarke From Love Island Trans
- Dress To Impress Creator Gigi
- B Cup Breast Size
- Julesari Leaks
Table of Contents
- Why Convert Decimals to Fractions Anyway?
- Converting Terminating Decimals to Fractions
- Converting Repeating Decimals to Fractions
- Why Precision Matters: The Problem with Floating-Point Numbers
- Tools and Techniques for Easier Conversion
- Common Questions About Decimal to Fraction Conversion
- Practice Makes Perfect!
Why Convert Decimals to Fractions Anyway?
You might be asking yourself, "Why bother learning how to convert decimals to fractions when calculators just give me decimals?" Well, it's a good question, and the answer really comes down to precision and clarity. Sometimes, a fraction just gives you a much clearer picture of a number than a long decimal does. For instance, knowing something is 1/3 is often more helpful than seeing 0.3333333, which is, you know, not perfectly exact.
My text also mentions that "floating point values can be imprecise." This is a big deal in areas like computer programming or science, where even tiny inaccuracies can add up. When you keep numbers in their fractional form, you maintain their exact value, so you never lose any information. It's like having the full recipe instead of just a summary, which is often better.
Also, fractions can make certain calculations simpler to see and do in your head. For example, multiplying by 1/2 is pretty straightforward, but multiplying by 0.5 might feel a bit different, even though it's the same thing. For many people, fractions just make more sense visually, which is a nice thing.
- Emily Compagno Husband
- What Does Wap Mean
- Do A Barrel Barrel Roll
- How Many Dogs Does Steve Horstmeyer Have
- How To Make Stickers
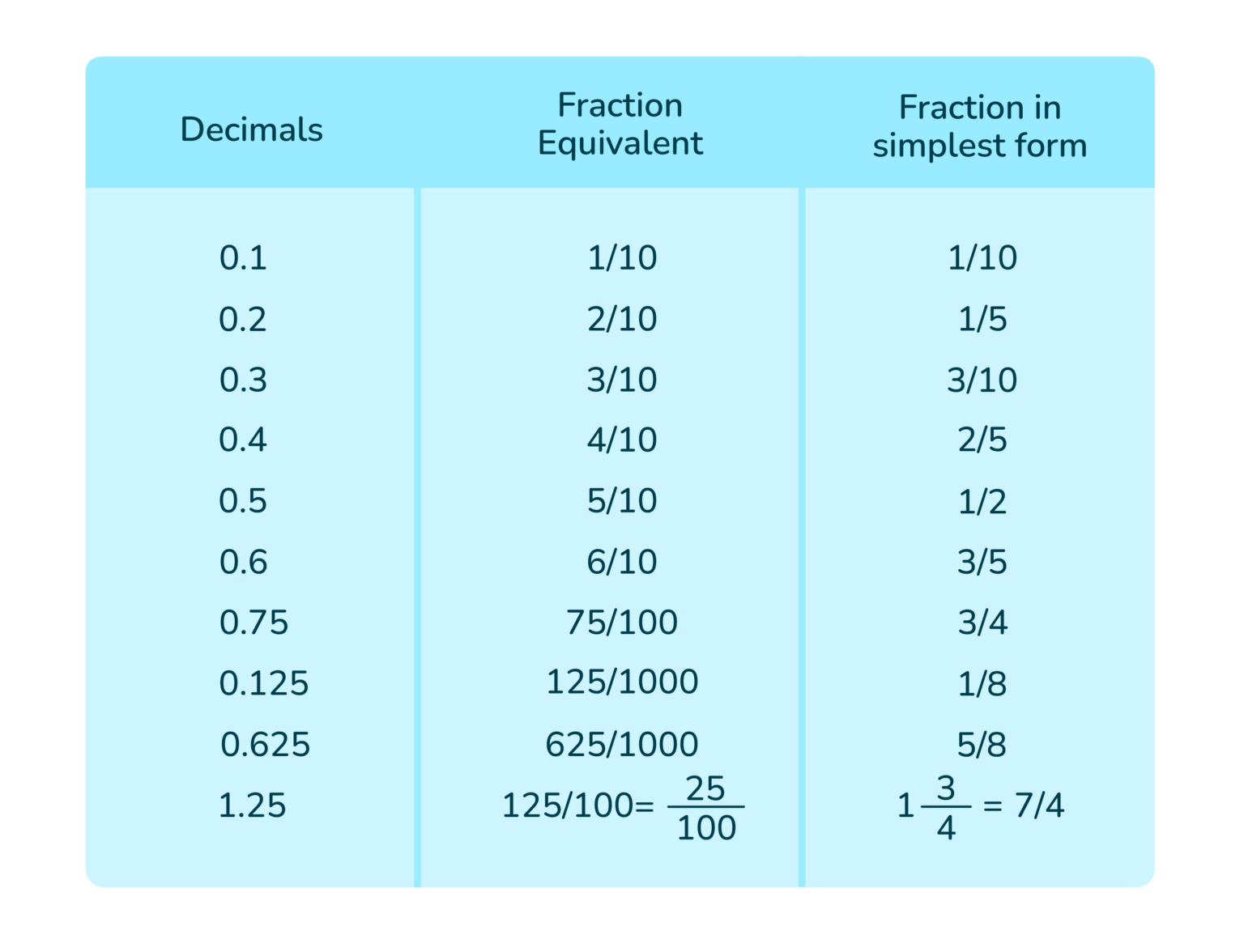
Converting Terminating Decimals to Fractions
Terminating decimals are the easiest kind to convert. These are decimals that, as the name suggests, stop. There is no endless string of numbers after the decimal point. Think of numbers like 0.25 or 0.7. They are pretty neat and tidy, actually.
Step-by-Step Guide for Terminating Decimals
Here is how you can change a terminating decimal into a fraction, so you can get a really clear number:
Write the decimal as a fraction over 1: Just put your decimal number on top of the number 1. For example, if you have 0.75, you would write it as 0.75/1. It's a simple start, you know.
Count the decimal places: Look at how many digits are after the decimal point. If it's 0.75, there are two digits (7 and 5). If it's 0.125, there are three digits. This count is pretty important.
Multiply the top and bottom by a power of 10: You want to get rid of the decimal point in the top number. To do this, multiply both the top and bottom of your fraction by 10 for every decimal place you counted. So, if there are two decimal places, you multiply by 100 (10^2). If there are three, you multiply by 1000 (10^3). This step makes the top number a whole number, which is good.
Simplify the fraction: Now you have a fraction with whole numbers on top and bottom. The last thing to do is simplify it to its lowest terms. Find the greatest common factor (GCF) of the top and bottom numbers and divide both by it. This makes the fraction as simple as it can be, which is often what you want.
Examples of Terminating Decimal Conversion
Let's walk through a couple of examples to make this really clear, so you can see it in action.
Example 1: Convert 0.4 to a fraction
Step 1: Write as 0.4/1.
Step 2: There is one decimal place (the 4).
Step 3: Multiply top and bottom by 10 (since there is one decimal place):
(0.4 * 10) / (1 * 10) = 4/10. It's almost there.Step 4: Simplify 4/10. The GCF of 4 and 10 is 2. Divide both by 2:
4 ÷ 2 = 2
10 ÷ 2 = 5
So, 0.4 as a fraction is 2/5. Pretty neat, right?
Example 2: Convert 0.125 to a fraction
Step 1: Write as 0.125/1.
Step 2: There are three decimal places (1, 2, and 5).
Step 3: Multiply top and bottom by 1000 (since there are three decimal places):
(0.125 * 1000) / (1 * 1000) = 125/1000. That's a bigger number, you know.Step 4: Simplify 125/1000. The GCF of 125 and 1000 is 125. Divide both by 125:
125 ÷ 125 = 1
1000 ÷ 125 = 8
So, 0.125 as a fraction is 1/8. It really simplifies down.
Converting Repeating Decimals to Fractions
Repeating decimals are a bit more involved, but still totally doable. These are decimals where one or more digits repeat endlessly, like 0.3333... (which is 0.3 with a line over the 3) or 0.1666... (0.16 with a line over the 6). My text mentions 0.1666667, which is 1/6, so we know this is a common one.
Step-by-Step Guide for Repeating Decimals
Here is how you can change a repeating decimal into a fraction, which is, you know, a very useful trick:
Set the decimal equal to a variable: Let's use 'x' for our decimal. So, if you have 0.333..., you would write x = 0.333... It's a good starting point.
Identify the repeating part: Figure out which digits are repeating. For 0.333..., it's just the '3'. For 0.121212..., it's '12'. This is a pretty key step.
Multiply by a power of 10 to move the repeating part past the decimal: Multiply 'x' by 10 raised to the power of how many digits are in the repeating block. If one digit repeats, multiply by 10. If two digits repeat, multiply by 100. This moves the decimal point so that the repeating part starts right after it. So, for x = 0.333..., you'd get 10x = 3.333.... For x = 0.1212..., you'd get 100x = 12.1212....
Subtract the original equation: Now, subtract your original equation (x = original decimal) from the new equation you just created. This step is a bit clever, as it makes the repeating part disappear. For example, if 10x = 3.333... and x = 0.333..., then 10x - x = 3.333... - 0.333..., which simplifies to 9x = 3. It's a rather neat trick.
Solve for x: You now have a simple equation like 9x = 3. Solve for 'x' by dividing both sides by the number next to 'x'. This will give you your fraction. So, x = 3/9.
Simplify the fraction: Just like with terminating decimals, simplify your fraction to its lowest terms. So, 3/9 simplifies to 1/3. That's the final step, you know.
Examples of Repeating Decimal Conversion
Let's look at some examples, so you can really get the hang of it.
Example 1: Convert 0.666... to a fraction
Step 1: Let x = 0.666...
Step 2: The repeating digit is '6'.
Step 3: Multiply by 10 (since one digit repeats):
10x = 6.666...Step 4: Subtract the original equation:
10x - x = 6.666... - 0.666...
9x = 6. It's pretty straightforward so far.Step 5: Solve for x:
x = 6/9Step 6: Simplify 6/9. The GCF of 6 and 9 is 3. Divide both by 3:
6 ÷ 3 = 2
9 ÷ 3 = 3
So, 0.666... as a fraction is 2/3. That's a good one.
Example 2: Convert 0.181818... to a fraction
Step 1: Let x = 0.181818...
Step 2: The repeating digits are '18'.
Step 3: Multiply by 100 (since two digits repeat):
100x = 18.181818... This makes a big jump.Step 4: Subtract the original equation:
100x - x = 18.181818... - 0.181818...
99x = 18. You can see the pattern, you know.Step 5: Solve for x:
x = 18/99Step 6: Simplify 18/99. The GCF of 18 and 99 is 9. Divide both by 9:
18 ÷ 9 = 2
99 ÷ 9 = 11
So, 0.181818... as a fraction is 2/11. It's a rather elegant solution.
Example 3: Convert 0.1666... to a fraction (a mixed repeating decimal)
Step 1: Let x = 0.1666...
Step 2: The repeating digit is '6', but there's a non-repeating '1' first. This is a bit different.
Step 3 (a): First, multiply by a power of 10 to get the non-repeating part before the decimal. Here, multiply by 10:
10x = 1.666...Step 3 (b): Now, multiply by another power of 10 to get one full repeating block before the decimal. Since '6' repeats (one digit), multiply 10x by 10 (which means x is multiplied by 100):
100x = 16.666...Step 4: Subtract the equation from Step 3 (a) from the equation from Step 3 (b). This is the key part to make the repeating decimal vanish:
100x - 10x = 16.666... - 1.666...
90x = 15. It really cleans things up.Step 5: Solve for x:
x = 15/90Step 6: Simplify 15/90. The GCF of 15 and 90 is 15. Divide both by 15:
15 ÷ 15 = 1
90 ÷ 15 = 6
So, 0.1666... as a fraction is 1/6. This shows how you handle those slightly more complex ones, you know.
Why Precision Matters: The Problem with Floating-Point Numbers
We have talked about precision a bit, but let's really think about it. My text mentions that "floating point values can be imprecise," and that you can "end up with 'weird' fractions." This is a rather big point, especially in computing.
Computers store numbers in binary, and just like 1/3 cannot be written perfectly as a decimal, many fractions cannot be written perfectly as binary floating-point numbers. This means that when a computer tries to represent a number like 0.1, it might actually store it as something like 0.09999999999999999 or 0.10000000000000001. These tiny differences are usually not a problem for everyday math, but for exact calculations, they can lead to errors. It's a subtle but important detail, you know.
This is why, as my text suggests, "for more clarity and precision, I would like to keep the fractional form instead of using floats." Keeping numbers as fractions means you retain their exact value, avoiding any rounding errors that might creep in with floating-point representations. This is particularly important when you are working with sensitive data or when results need to be perfectly accurate, like in financial calculations or scientific modeling, so it's a good habit to get into.
Tools and Techniques for Easier Conversion
While the manual steps are great for understanding, sometimes you need a quicker way, especially in programming. My text mentions struggling to find a simple method and wanting a function that takes a "double value and return a string" for a larger program. It also brings up the 'fractions' module in Python, which is a powerful tool.
For example, in Python, the `fractions` module can help you convert decimals to fractions directly. You can create a `Fraction` object from a decimal. My text also points out that you might get "weird" fractions from imprecise floats, and suggests using `fraction.limit_denominator()`. This is a really helpful feature. It lets you tell the program to find the closest fraction with a denominator (the bottom number) no larger than a certain value. This can make those "weird" fractions much more readable and practical. It's a nice way to simplify things, you know.
So, instead of getting something like 3602879701896397/11258999068426240 for a slightly off decimal, `limit_denominator(100)` might give you 1/3 or 7/50, which is far more useful. This kind of tool helps you get the precision you need without the overly complex output. You can learn more about Python's fractions module here, which is a pretty good resource.
If you are working with spreadsheets, some programs offer custom formatting options to display numbers as fractions. My text even mentions using custom Excel format strings in DAX with the `FORMAT` function. While this might just be about how the number *looks* rather than its actual underlying value, it shows the desire to see numbers in their fractional form for clarity. This is often just about presentation, but it still helps with how you understand the data, you know?
Common Questions About Decimal to Fraction Conversion
People often have similar questions when they are learning how to convert decimals to fractions. Here are some of the most common ones, so you can get some quick answers.
What is the easiest way to convert a decimal to a fraction?
For terminating decimals, the easiest way is to write the decimal over a power of 10 (like 10, 100, 1000, depending on decimal places) and then simplify. For example, 0.75 is 75/100, which simplifies to 3/4. This is usually the most straightforward approach, you know.
How do you convert a decimal with a repeating pattern to a fraction?
You set the decimal equal to 'x', then multiply 'x' by a power of 10 to shift the repeating part. Subtract the original equation from the new one to eliminate the repeating digits, and then solve for 'x'. This method works for all repeating decimals, even the mixed ones. It's a very reliable method.
Why do some decimals give "weird" fractions when converted by a computer?
This happens because computers use floating-point numbers, which can be imprecise. Just like 1/3 can't be perfectly written as a decimal, many decimals can't be perfectly represented in binary. When a computer tries to convert an imprecise decimal back to a fraction, it might give a very long, complex fraction that is technically correct for the *stored* (but slightly off) value, rather than the exact fraction you might expect. This is why using tools like `limit_denominator` or starting with exact fractions is often better, you know, for avoiding those issues.
Practice Makes Perfect!
The best way to get good at how to convert decimals to fractions is to practice. Take different decimal numbers, both terminating and repeating, and work through the steps. You will find that with a little bit of effort, it becomes much easier and more intuitive. This skill really helps you understand numbers better, and it gives you a powerful tool for precision in many different areas of life, so it's worth the time. You can learn more about number systems on our site, and also check out this page for additional math resources to help you along.
- Ball Up Top Meaning
- Brandi Passante Pics
- Blowout Taper Straight Hair
- Sophie Rain Spiderman Vid
- Just Give Me My Money

Free worksheet convert fractions to decimals, Download Free worksheet
How to Convert Decimals to Fractions - DoodleLearning

Fraction-decimal Chart in Illustrator, PDF - Download | Template.net