Unlocking The Perimeter Of A Formula: Your Guide To Shapes And Spaces

Have you ever looked at a garden, a room, or even just a picture frame and wondered how much "edge" it has? Well, that feeling, that curiosity about the boundary around something, is actually pretty common, you know. It's a fundamental idea in geometry, and it pops up in our daily lives more often than we might think, actually. Figuring out these edges, or boundaries, is what we call finding the perimeter.

So, what exactly is the perimeter of a formula, you might ask? It’s not about the formula itself having an edge, but rather about using specific mathematical instructions – the formulas – to measure the total distance around the outside of a flat shape. It's like walking along the very edge of a park; the total distance you walk is the park's perimeter, and a formula helps you figure that out without needing to walk it every single time, which is pretty handy, right?

Today, we're going to take a closer look at these amazing formulas. We'll explore what perimeter truly means, how it helps us in practical situations, and how different shapes, you know, have their own special ways of calculating this important measurement. It's all about understanding the outlines of the world around us, and how a simple formula can make that task much, much easier, more or less.

• Burger King Crown Guy
• How To See Deleted Sms
• Michael B Jordan Girlfriend
• La Casa De Los Famosos Vota
• Wasmo Somali Channel Telegram 2025

Table of Contents

• What is Perimeter, Really?
• Why Perimeter Matters in Your Everyday
• Common Shapes and Their Perimeter Formulas
  • Squares and Rectangles: The Basics
  • Triangles: Three Sides of Fun
  • Circles: A Special Kind of Perimeter (Circumference)
  • Other Polygons: Many Sides, Many Sums
• Tackling Tricky Shapes and Optimization
• Frequently Asked Questions About Perimeter
• Putting Perimeter to Work: Your Next Steps

What is Perimeter, Really?

So, at its heart, perimeter is just the total distance around the outside edge of a two-dimensional shape. Think of it like a fence around a yard, or the border of a picture, or even, you know, the very rim of a cup. It's that outer boundary, the path you'd trace if you were walking all the way around something, and then, you know, came back to where you started. My text actually puts it quite simply, saying 'perimeter' defines the outline of a figure, which is pretty accurate, you see.

Now, it's pretty important to understand that perimeter applies to what we call "closed shapes," so, you know, shapes where the lines connect all the way around. For instance, if you have a square or a rectangle, you can definitely find its perimeter. If you have, say, just a single line segment, there's no perimeter to measure there, is there? It's all about the enclosure, more or less.

And here's a little distinction, too. While "perimeter" is a general term for the distance around most two-dimensional shapes, when we talk specifically about circles, we use a different word: "circumference." My text explains this nicely, saying "Circumference is the distance around a circle," while "Perimeter is the distance around other 2 dimensional shapes." So, it's just a special name for the perimeter of a circle, you know, a bit like how a dog is a pet, but a golden retriever is a specific kind of dog, basically.

• Kendrick Lamar Mustard Song
• Is A Fish An Animal
• How To Ripen Avocados
• How Did Mr Beast Get Rich
• Kimberly Guilfoyle Before And After

Why Perimeter Matters in Your Everyday

You might be thinking, "Why do I even need to know about the perimeter of a formula?" Well, as a matter of fact, this concept pops up in so many practical situations, it's almost surprising. It's not just for math class, you know. Think about, say, home improvement projects. If you're putting up a fence around your garden, you absolutely need to know the perimeter to buy the right amount of fencing material. My text even uses this exact example: "The gardener had to measure the perimeter of the garden to buy the right amount of fencing," which is a very real-world scenario, you see.

Or what about, say, decorating a room? If you want to add a decorative border around the top of your walls, you'll need the room's perimeter to figure out how much border to purchase. Similarly, if you're framing a picture, the length of the frame material needed is, you guessed it, the perimeter of the picture. It's really quite useful, you know, for avoiding buying too much or too little material, which can save you time and money, actually.

Even things like sports fields or running tracks are designed using perimeter measurements. The length of a lap on a track is essentially its perimeter. Knowing these measurements helps athletes train effectively and ensures fair competition. So, you know, whether it's for building, crafting, or even just playing, understanding the perimeter of a formula is, in fact, a very practical skill to have, more or less.

Common Shapes and Their Perimeter Formulas

Now, let's get into the heart of it: how do we actually calculate this perimeter for different shapes? Each shape, you know, has its own specific formula, but the core idea is always the same: add up the lengths of all the sides. The formulas just give us a quick way to do that, especially for shapes with regular patterns, you know, like squares or rectangles.

Squares and Rectangles: The Basics

These are probably the easiest shapes to start with, honestly. A square has four sides, and all of them are the exact same length. So, to find its perimeter, you could just add side + side + side + side. But, you know, there's a simpler way, a formula, if you will. If 's' stands for the length of one side, then the perimeter (P) of a square is just:

• P = 4 × s

For example, my text mentions a square S1 with a perimeter of 40 inches. If P = 40, then 40 = 4 × s, which means s = 10 inches. Pretty straightforward, right?

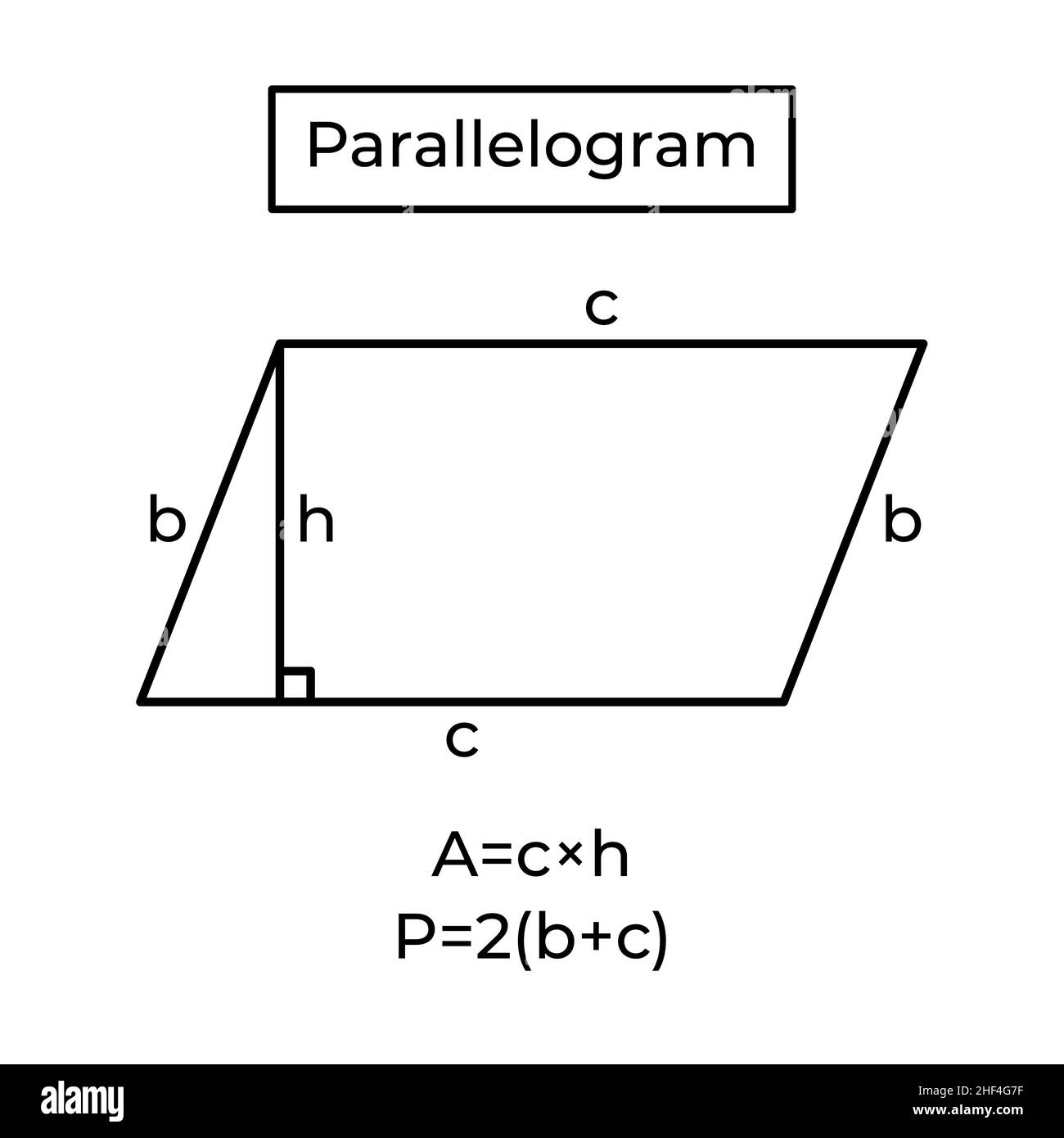
Rectangles are pretty similar, but they have two pairs of equal sides: a length (l) and a width (w). So, you have two lengths and two widths. To find the perimeter (P) of a rectangle, you'd add length + width + length + width. The formula makes it a bit quicker:

• P = 2 × (l + w) or P = 2l + 2w

This is really useful, you know, if you're trying to figure out how much trim you need for a rectangular room, for instance. It's just a quicker way to do the addition, basically.

Triangles: Three Sides of Fun

Triangles are, you know, shapes with three sides. And because those three sides can be all different lengths, or some the same, the formula for a triangle's perimeter is very, very simple: you just add up the lengths of its three sides. If the sides are 'a', 'b', and 'c', then the perimeter (P) is:

• P = a + b + c

It doesn't matter if it's an equilateral triangle (all sides equal), an isosceles triangle (two sides equal), or a scalene triangle (all sides different); the principle remains the same. You just measure each side and, you know, add them all together. It's as simple as that, more or less.

Circles: A Special Kind of Perimeter (Circumference)

As we talked about earlier, the perimeter of a circle has its own special name: circumference. And since circles don't have straight sides to add up, their formula is a bit different, too it's almost. It involves a very special number called Pi (π), which is approximately 3.14159. The circumference (C) of a circle depends on its radius (r) or its diameter (d). The diameter is just twice the radius (d = 2r).

• C = 2 × π × r (if you know the radius)
• C = π × d (if you know the diameter)

This is how you figure out, say, the length of the edge of a round table or the distance around a circular track. It's a bit more abstract than adding sides, but it's really quite precise, you know, once you get the hang of using Pi, basically. Learn more about basic geometric shapes on our site.

Other Polygons: Many Sides, Many Sums

For any other polygon – that's just a fancy word for a closed shape with straight sides – the rule for finding the perimeter is just like with triangles: you add up the lengths of all its sides. Whether it's a pentagon (5 sides), a hexagon (6 sides), or an octagon (8 sides), the formula for the perimeter (P) is:

• P = sum of all side lengths

So, if you have a pentagon with sides a, b, c, d, and e, its perimeter is P = a + b + c + d + e. If it's a regular polygon, meaning all its sides are the same length, and it has 'n' sides, and each side has length 's', then the formula simplifies to P = n × s. It's all about adding up those edges, you know, no matter how many there are, more or less.

Tackling Tricky Shapes and Optimization

Sometimes, shapes aren't just simple squares or circles. My text, actually, has some pretty interesting problems that combine different shapes, like a window that's a rectangle topped by a semicircle. Or, you know, a pentagon formed by a triangle on a rectangle. For these kinds of composite shapes, you'd find the perimeter by adding up the lengths of all the *outer* edges, carefully avoiding any internal lines that aren't part of the boundary, which is pretty important, you see.

A really common challenge, too it's almost, is what we call "optimization problems." This is where you're given a fixed perimeter, say 100 inches, and you need to find the dimensions of a shape that will give you the largest possible area. My text has a problem like this: "Find the dimensions x and y that maximize the area given that the perimeter is 100." This kind of problem often involves a bit of algebra and calculus, but the core idea still relies on those perimeter formulas, you know.

For example, if you have 100 feet of fence, you might want to know what shape of garden (rectangle, square, etc.) will give your plants the most space inside. It turns out, a circle usually gives the most area for a given perimeter, but if you're stuck with a rectangular shape, a square is usually your best bet. These problems show that the perimeter of a formula isn't just about measuring; it's also about, you know, making the most of what you have, which is pretty clever, honestly. You can find more detailed examples of these problems and their solutions on pages like Math Is Fun, for instance.

Another interesting problem from my text talks about a rectangular piece of sheet metal with a perimeter of 50cm being rolled into a cylinder. Here, the perimeter of the rectangle becomes part of the cylinder's dimensions, like its circumference or height. It's a way of seeing how perimeter measurements, you know, can transform from one context to another, which is pretty fascinating, basically. And it really highlights how interconnected these geometric ideas are, more or less. To learn more about advanced geometric applications, check out this page.

Frequently Asked Questions About Perimeter

What is the basic formula for perimeter?

The most basic idea for finding the perimeter of any polygon is just to add up the lengths of all its outside edges. So, if a shape has sides a, b, c, and so on, its perimeter is P = a + b + c + ... For circles, it's called circumference, and the formula is C = 2πr or C = πd, you know, using the radius or diameter, which is pretty specific, actually.

How do you find the perimeter of a complex shape?

For shapes that are, you know, made up of several simpler shapes, you just need to carefully identify and then add up the lengths of all the *outer* boundaries. You might need to use different formulas for different parts, like a straight line segment and then, say, a curved arc from a circle. It's all about, you know, being methodical and making sure you don't miss any outside edges or count any inside ones, which is important, basically.

What's the difference between perimeter and area?

This is a really good question, you know, and people often mix them up. Perimeter is the total distance around the outside edge of a shape, like the fence around a yard. Area, on the other hand, is the amount of surface *inside* that shape, like the grass within the fenced yard. So, one is a length measurement (perimeter), and the other is a measurement of space or surface (area). They're related, but they measure very different things, more or less.

Putting Perimeter to Work: Your Next Steps

So, you know, we've gone over quite a bit about the perimeter of a formula today. From the simple act of adding up sides to tackling more complex shapes and even optimization challenges, this fundamental concept is, in fact, a cornerstone of geometry and a very useful tool in everyday life. Whether you're planning a garden, designing a room, or just trying to understand the world around you a bit better, knowing how to calculate perimeter is a really valuable skill to have, basically.

The next time you see a shape, you might just find yourself, you know, mentally tracing its outline and thinking about its perimeter. It's a great way to practice and solidify what you've learned. So, why not try to measure the perimeter of something in your home right now? Maybe your desk, or a book, or even your phone. It’s a fun way to put these formulas to the test, honestly, and see how they apply to the real things you interact with every single day, more or less.

• How To Erase Gel Nail Polish
• Abbey Love On The Spectrum
• In The Clerb We All Fam
• Nice And Slow Lyrics
• Jackerman Mother Warmth

Details

Solved: Formula Perimeter [algebra]

Details

Area And Perimeter Formula Deep Discounts | www.pinnaxis.com

Details

Perimeter Formula