Home / Tiktok Talks 002

How To Do Long Division: Your Guide To Breaking Down Big Numbers

Vidal Witting

Ever look at a really big number and wonder how you could ever split it up fairly among a group? That, is that feeling many people get when they think about long division. It's a skill that seems complex at first glance, but it's actually one of the most practical things you can learn in math. It helps us solve everyday problems, from sharing cookies equally to figuring out finances, so it's really useful.

Long division, you know, is a way of working through division problems that have numbers with at least two digits. It’s a core part of basic arithmetic, helping us find the answer and any leftover bits when we divide. My text tells us it’s a methodical approach, a step-by-step way of doing things that efficiently breaks down big numbers into smaller, more manageable pieces. There are full versions of the process, and sometimes you see shortened ones, but the basic idea stays the same.

Whether you’re a student just starting out, or maybe you just need a little refresher, this article is here to help. We're going to learn how to divide using this long division method, along with some examples that show all the steps. We'll go through it all, making sure you get a good grip on how to do long division, because everyone needs a refresher from time to time, right?

Table of Contents

What is Long Division, Anyway?

My text tells us that long division is a way of solving and finding the answer and remainder for division problems that involve numbers with at least two digits. It’s a foundational arithmetic operation, really, that takes large numbers and breaks them into smaller, more manageable parts. Think of it like this: if you have a big pile of something and you need to split it into equal smaller piles, long division helps you figure out exactly how much goes into each pile, and if anything is left over. It’s a very organized way to do this, actually.

Basically, it helps us work with bigger numbers than we might easily do in our heads. We often see it written out in a specific way, with the numbers arranged under a special symbol, which helps keep all the steps clear. It’s a step-by-step process where you look at the values at each place, like the thousands, hundreds, tens, and ones, and you divide them one at a time, starting with the biggest place value first. This systematic approach is what makes it so effective for complex problems, you know.

Why Learning How to Do Long Division Matters

Knowing how to do long division is, in math, one of those skills that is very practical. My text points out that it's the way we break down complex problems into steps that are easy to handle. This makes it a really important tool for many things. It’s not just for school assignments; it helps us in real life, too. For instance, if you’re planning a trip and need to figure out how many miles per gallon your car gets, or if you’re trying to split a restaurant bill evenly with friends, long division is there to help.

It builds a strong base for other math skills you might learn later, like algebra or even some higher-level calculations. For someone like a 4th-grade student, it can seem like a mix of different operations, so reviewing the basic skills is important for them to learn it well. But it’s not just for kids; anyone needing to work with numbers in a detailed way finds it useful. It helps you think through problems in an orderly fashion, which is a great skill to have in general, you know.

Getting Ready for Long Division

Before you jump right into the full long division process, it helps to make sure you’re comfortable with a few basic ideas. It’s a bit like getting your tools ready before you start building something. A little preparation can make the whole experience much smoother, honestly. We’ll look at the parts of a division problem and then quickly go over some math skills you’ll want to have handy, because, well, they are pretty much the building blocks.

Understanding the Parts of a Division Problem

Every division problem has three main parts, and knowing what they are called makes it easier to follow the steps of long division. My text mentions that to divide 24 by 4, we write 24 ÷ 4. In this simple example, we have:

  • The **Dividend**: This is the total amount you are dividing. It’s the number being split up. In 24 ÷ 4, the dividend is 24.
  • The **Divisor**: This is the number that tells you how many equal groups you are making, or how many are in each group. It’s the number you are dividing by. In 24 ÷ 4, the divisor is 4.
  • The **Quotient**: This is the answer to your division problem. It tells you how many are in each group, or how many groups you have. For 24 ÷ 4, the quotient is 6.
  • The **Remainder**: Sometimes, when you divide, there’s a little bit left over that can’t be divided evenly. This leftover part is called the remainder. Not every problem has one, but many do, you know.

Understanding these terms will make it much simpler to follow along with the steps that are coming up, as a matter of fact.

A Quick Review of Basic Math Skills

To do long division well, it’s really helpful to be good at a few other basic math operations. Think of these as your warm-up exercises. You’ll be using them a lot throughout the process, so a little practice here goes a long way. These skills include:

  • **Multiplication Facts**: Knowing your multiplication tables quickly will speed up the process a lot. You’ll be multiplying numbers in almost every step.
  • **Subtraction**: You’ll need to subtract numbers correctly to find out what’s left after each division step. This is a pretty big part of it.
  • **Basic Division Facts**: Knowing simple division facts, like 20 divided by 5 is 4, helps you estimate and start each step of long division. It gives you a good starting point, basically.

If any of these feel a little rusty, it’s a good idea to spend a little time brushing up on them. They are, after all, the foundation for long division, so a strong base helps a lot.

The Step-by-Step Process for How to Do Long Division

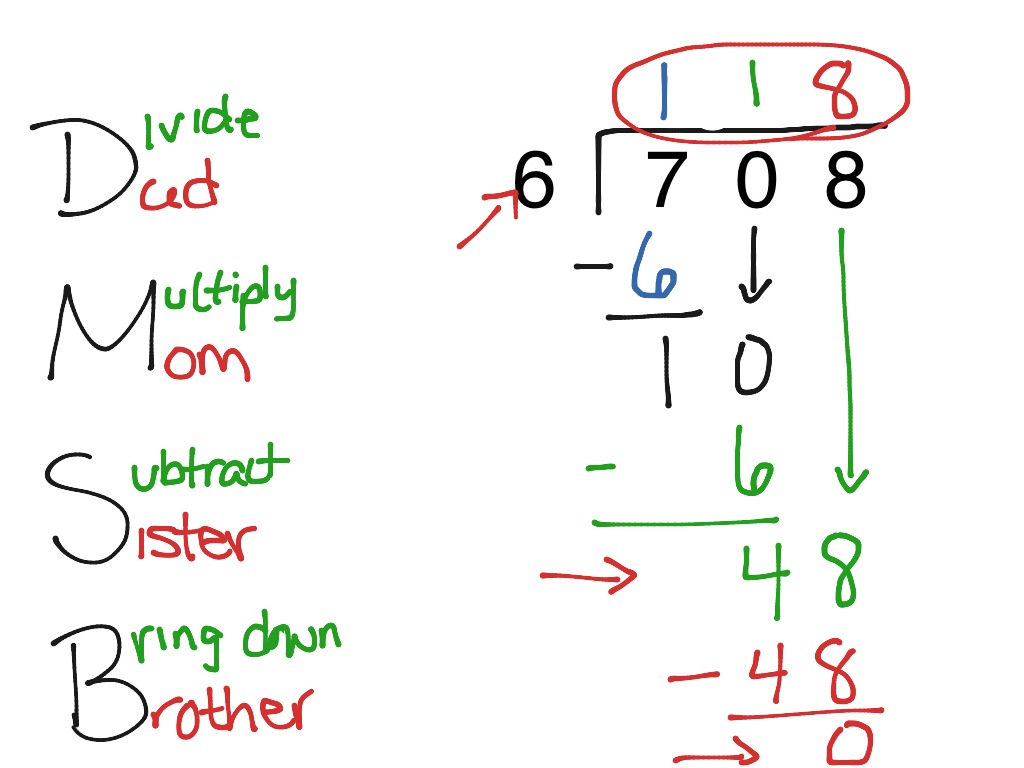
Now, let's get into the heart of how to do long division. We'll go through each step, one by one. Remember, my text says that in long division, you divide values at each individual place – thousands, hundreds, tens, ones – starting with the highest place. This is a very systematic way to approach it. We'll use a common acronym, "Does McDonald's Sell Burgers?" or "DMSB," to help you remember the order: Divide, Multiply, Subtract, Bring Down. Then you repeat. It's a handy little trick, you know.

Step 1: Divide

This is where you start. Look at the first digit or first few digits of your dividend, from left to right. You want to see how many times your divisor can fit into that part of the dividend without going over. You write this number, which is part of your quotient, right above the digit you just used in the dividend. For instance, if you're dividing 84 by 4, you first look at the 8. How many times does 4 go into 8? It goes in 2 times. So, you write 2 above the 8. It’s pretty straightforward to begin with.

Step 2: Multiply

Once you've figured out how many times the divisor fits, you multiply that number (the one you just wrote in the quotient) by the divisor. You then write this product directly below the part of the dividend you were just working with. Going back to our 84 divided by 4 example: you put 2 above the 8. Now, you multiply that 2 by your divisor, which is 4. So, 2 times 4 equals 8. You write this 8 right below the 8 in the dividend. This step, you know, confirms your division choice.

Step 3: Subtract

After you've multiplied, your next move is to subtract the number you just wrote (the product) from the part of the dividend above it. The result of this subtraction should always be less than your divisor. If it’s not, it means you picked a number that was too small in the divide step, and you need to go back and try a larger number. In our example, you subtract 8 from 8, which leaves you with 0. This zero is important; it shows what's left over before you bring down the next digit, basically.

Step 4: Bring Down

Now you bring down the next digit from the dividend and place it next to the result of your subtraction. This creates a new number that you’ll work with for the next round of dividing. So, with 84 divided by 4, after subtracting 8 from 8 to get 0, you bring down the 4 from the dividend. You now have 04, which is just 4, as your new number to divide. This step is what makes the process continue, you know, allowing you to deal with the whole dividend.

Step 5: Repeat or Find the Remainder

With your new number (the one you got after bringing down), you go back to Step 1 and repeat the whole process: Divide, Multiply, Subtract, Bring Down. You keep doing this until there are no more digits left in the dividend to bring down. If, after your last subtraction, you have a number left over that is smaller than your divisor, that number is your remainder. If the final subtraction leaves you with 0 and there are no more digits, then you have no remainder. It's a cycle, really, until the problem is finished, and you know, that's how it works.

Long Division Example: A Walkthrough

Let's walk through a couple of examples to really see how these steps fit together. Sometimes seeing it done makes all the difference, right? We'll start with a simpler one and then move to something a little more involved. This way, you can get a good feel for how to do long division with different kinds of numbers. These examples will show the long division steps in action, as my text suggests, with answers.

Example 1: Dividing a 3-Digit Number by a 1-Digit Number

Let's divide 567 by 3. We'll set it up like this:

 ____ 3 | 567

**Step 1: Divide**

  • Look at the first digit of the dividend, which is 5. How many times does 3 go into 5? It goes in 1 time (because 3 x 1 = 3, and 3 x 2 = 6, which is too big). Write 1 above the 5.
 1___ 3 | 567

**Step 2: Multiply**

  • Multiply the number you just wrote (1) by the divisor (3). 1 x 3 = 3. Write 3 below the 5.
 1___ 3 | 567 3

**Step 3: Subtract**

  • Subtract 3 from 5. 5 - 3 = 2. Write 2 below the 3.
 1___ 3 | 567 -3 --- 2

**Step 4: Bring Down**

  • Bring down the next digit from the dividend, which is 6, and place it next to the 2. You now have 26.
 1___ 3 | 567 -3 --- 26

**Step 5: Repeat (Divide again)**

  • Now, how many times does 3 go into 26? Think about your multiplication facts. 3 x 8 = 24, and 3 x 9 = 27 (too big). So, it goes in 8 times. Write 8 next to the 1 in the quotient, above the 6.
 18__ 3 | 567 -3 --- 26

**Multiply again**

  • Multiply the new quotient digit (8) by the divisor (3). 8 x 3 = 24. Write 24 below the 26.
 18__ 3 | 567 -3 --- 26 24

**Subtract again**

  • Subtract 24 from 26. 26 - 24 = 2. Write 2 below the 24.
 18__ 3 | 567 -3 --- 26 -24 --- 2

**Bring Down again**

  • Bring down the last digit from the dividend, which is 7, and place it next to the 2. You now have 27.
 18_ 3 | 567 -3 --- 26 -24 --- 27

**Repeat (Divide one more time)**

  • How many times does 3 go into 27? 3 x 9 = 27. So, it goes in 9 times. Write 9 next to the 8 in the quotient, above the 7.
 189 3 | 567 -3 --- 26 -24 --- 27

**Multiply again**

  • Multiply the new quotient digit (9) by the divisor (3). 9 x 3 = 27. Write 27 below the 27.
 189 3 | 567 -3 --- 26 -24 --- 27 27

**Subtract again**

  • Subtract 27 from 27. 27 - 27 = 0. Write 0 below the 27.
 189 3 | 567 -3 --- 26 -24 --- 27 -27 --- 0

**Find the Remainder**

  • There are no more digits to bring down, and our final subtraction result is 0. So, the remainder is 0. The answer (quotient) is 189.

So, 567 divided by 3 is 189 with no remainder. That, is how you do it step by step.

Example 2: Dividing a 4-Digit Number by a 2-Digit Number

Let's try a slightly bigger one: 4,325 divided by 12. This one involves a two-digit divisor, so it’s a bit more challenging, you know, but the steps are exactly the same. Setting it up:

 ____ 12 | 4325

**Step 1: Divide**

  • Look at the first digit of the dividend, 4. Can 12 go into 4? No. So, look at the first two digits, 43. How many times does 12 go into 43? 12 x 3 = 36, and 12 x 4 = 48 (too big). So, it goes in 3 times. Write 3 above the 3 in 43.
 _3__ 12 | 4325

**Step 2: Multiply**

  • Multiply the quotient digit (3) by the divisor (12). 3 x 12 = 36. Write 36 below 43.
 _3__ 12 | 4325 36

**Step 3: Subtract**

  • Subtract 36 from 43. 43 - 36 = 7. Write 7 below the 36.
 _3__ 12 | 4325 -36 --- 7

**Step 4: Bring Down**

  • Bring down the next digit from the dividend, which is 2, and place it next to the 7. You now have 72.
 _3__ 12 | 4325 -36 --- 72

**Step 5: Repeat (Divide again)**

  • How many times does 12 go into 72? 12 x 5 = 60, 12 x 6 = 72. So, it goes in 6 times. Write 6 next to the 3 in the quotient, above the 2.
 36__ 12 | 4325 -36 --- 72

**Multiply again**

  • Multiply the new quotient digit (6) by the divisor (12). 6 x 12 = 72. Write 72 below the 72.
 36__ 12 | 4325 -36 --- 72 72

**Subtract again**

  • Subtract 72 from 72. 72 - 72 = 0. Write 0 below the 72.
 36__ 12 | 4325 -36 --- 72 -72 --- 0

**Bring Down again**

  • Bring down the last digit from the dividend, which is 5, and place it next to the 0. You now have 05, which is just 5.
 36_ 12 | 4325 -36 --- 72 -72 --- 05

**Repeat (Divide one more time)**

  • How many times does 12 go into 5? It goes in 0 times (since 12 is bigger than 5). Write 0 next to the 6 in the quotient, above the 5.
 360 12 | 4325 -36 --- 72 -7
Long Division Steps And Examples

Long Division Steps And Examples

Long Division Video – Corbettmaths Primary

Long Division Video – Corbettmaths Primary

Steps For Long Division Printable

Steps For Long Division Printable

Detail Author:

  • Name : Vidal Witting
  • Username : parisian.austin
  • Email : ashlee.homenick@gutkowski.com
  • Birthdate : 2006-01-24
  • Address : 708 Heaney Mountains Stammton, IN 01538-5758
  • Phone : +1-660-242-6278
  • Company : Wehner, Klocko and Christiansen
  • Job : Marine Engineer
  • Bio : Rerum iusto voluptate consequuntur sequi quisquam saepe. Neque aut quis accusamus eum doloremque nam at. Voluptatem doloribus pariatur qui.

Socials

instagram:

  • url : https://instagram.com/wilfredo.littel
  • username : wilfredo.littel
  • bio : Aliquid atque sed est. Sequi natus officiis laudantium consectetur blanditiis.
  • followers : 1582
  • following : 965

facebook:

  • url : https://facebook.com/wilfredo_littel
  • username : wilfredo_littel
  • bio : Odio non at qui. Eius esse quibusdam eaque repudiandae cupiditate id sunt.
  • followers : 3521
  • following : 1639